
【題目】已知圓C:![]() 及點P(0,1),過點P的直線與圓交于A、B兩點.
及點P(0,1),過點P的直線與圓交于A、B兩點.
(1)若弦長![]() 求直線AB的斜率;
求直線AB的斜率;
(2)求△ABC面積的最大值,及此時弦長![]()
科目:高中數學 來源: 題型:
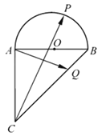
【題目】如圖,在等腰直角三角形ABC中,∠CAB=90°,AB=2,以AB為直徑在△ABC外作半圓O,P為半圓弧AB上的動點,點Q在斜邊BC上,若![]() =
=![]() ,則
,則![]() 的最小值為_______.
的最小值為_______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雞的產蛋量與雞舍的溫度有關,為了確定下一個時段雞舍的控制溫度,某企業需要了解雞舍的溫度![]() (單位:℃),對某種雞的時段產蛋量
(單位:℃),對某種雞的時段產蛋量![]() (單位:
(單位: ![]() )和時段投入成本
)和時段投入成本![]() (單位:萬元)的影響,為此,該企業收集了7個雞舍的時段控制溫度
(單位:萬元)的影響,為此,該企業收集了7個雞舍的時段控制溫度![]() 和產蛋量
和產蛋量![]() 的數據,對數據初步處理后得到了如圖所示的散點圖和表中的統計量的值.
的數據,對數據初步處理后得到了如圖所示的散點圖和表中的統計量的值.

|
|
|
|
|
|
|
17.40 | 82.30 | 3.6 | 140 | 9.7 | 2935.1 | 35.0 |
其中![]() .
.
(1)根據散點圖判斷, ![]() 與
與![]() 哪一個更適宜作為該種雞的時段產蛋量
哪一個更適宜作為該種雞的時段產蛋量![]() 關于雞舍時段控制溫度
關于雞舍時段控制溫度![]() 的回歸方程類型?(給判斷即可,不必說明理由)
的回歸方程類型?(給判斷即可,不必說明理由)
(2)若用![]() 作為回歸方程模型,根據表中數據,建立
作為回歸方程模型,根據表中數據,建立![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(3)已知時段投入成本![]() 與
與![]() 的關系為
的關系為![]() ,當時段控制溫度為28℃時,雞的時段產蛋量及時段投入成本的預報值分別是多少?
,當時段控制溫度為28℃時,雞的時段產蛋量及時段投入成本的預報值分別是多少?
附:①對于一組具有有線性相關關系的數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為
②
|
|
|
|
|
0.08 | 0.47 | 2.72 | 20.09 | 1096.63 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】己知p:函數f(x)在R上是增函數,f(m2)<f(m+2)成立;q:方程![]() 1(m∈R)表示雙曲線.
1(m∈R)表示雙曲線.
(1)若p為真命題,求m的取值范圍;
(2)若p∨q為真,p∧q為假,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
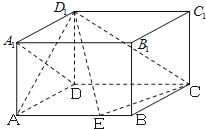
【題目】已知在長方體ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,點E在棱AB上移動.
(Ⅰ)求證:D1E⊥A1D;
(Ⅱ)在棱AB上是否存在點E使得AD1與平面D1EC成的角為![]() ?若存在,求出AE的長,若不存在,說明理由.
?若存在,求出AE的長,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于無窮數列![]() ,若正整數
,若正整數![]() ,使得當
,使得當![]() 時,有
時,有![]() ,則稱
,則稱![]() 為“
為“![]() 不減數列”.
不減數列”.
(1)設![]() ,
,![]() 均為正整數,且
均為正整數,且![]() ,甲:
,甲:![]() 為“
為“![]() 不減數列”,乙:
不減數列”,乙:![]() 為“
為“![]() 不減數列”.試判斷命題:“甲是乙的充分條件”的真假,并說明理由;
不減數列”.試判斷命題:“甲是乙的充分條件”的真假,并說明理由;
(2)已知函數![]() 與函數
與函數![]() 的圖象關于直線
的圖象關于直線![]() 對稱,數列
對稱,數列![]() 滿足
滿足![]() ,
,![]() ,如果
,如果![]() 為“
為“![]() 不減數列”,試求
不減數列”,試求![]() 的最小值;
的最小值;
(3)對于(2)中的![]() ,設
,設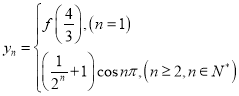 ,且
,且![]() .是否存在實數
.是否存在實數![]() 使得
使得![]() 為“
為“![]() 不減數列”?若存在,求出
不減數列”?若存在,求出![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com