
分析 (Ⅰ)由條件利用等比數列的定義和性質,求得數列{an}為首項等于1、公比為q的等比數列,
(Ⅱ)根據2a2,a3,a2+2成等差數列求得公比q的值,可得{an}的通項公式.
解答 解:(Ⅰ)證明:∵Sn+1=qSn+1 ①,
∴當n≥2時,Sn=qSn-1+1 ②,兩式相減可得an+1=q•an,
即從第二項開始,數列{an}為等比數列,公比為q.
當n=1時,
∵數列{an}的首項為1,
∴a1+a2=S2=q•a1+1,
∴a2 =a1•q,
∴數列{an}為等比數列,公比為q.
(Ⅱ)∵2a2,a3,a2+2成等差數列,
∴2a3 =2a2+a2+2,∴2q2=2q+q+2,求得q=2,或 q=-$\frac{1}{2}$.
根據q>0,故取q=2,
∴an=2n-1,n∈N*.
點評 本題主要考查等差數列、等比數列的定義和性質,以及數列的遞推公式,屬于中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 16 | B. | 72 | C. | 37 | D. | 100 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
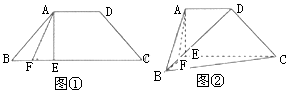 如圖①所示,四邊形ABCD為等腰梯形,AD∥BC,且AD=$\frac{1}{3}$BC=a,∠BAD=135°,AE⊥BC于點E,F為BE的中點.將△ABE沿著AE折起至△AB′E的位置,得到如圖②所示的四棱錐B′-ADCE.
如圖①所示,四邊形ABCD為等腰梯形,AD∥BC,且AD=$\frac{1}{3}$BC=a,∠BAD=135°,AE⊥BC于點E,F為BE的中點.將△ABE沿著AE折起至△AB′E的位置,得到如圖②所示的四棱錐B′-ADCE.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com