
【題目】已知![]() 是整數,冪函數
是整數,冪函數![]() 在
在![]() 上是單調遞增函數.
上是單調遞增函數.

(1)求冪函數![]() 的解析式;
的解析式;
(2)作出函數![]() 的大致圖象;
的大致圖象;
(3)寫出![]() 的單調區間,并用定義法證明
的單調區間,并用定義法證明![]() 在區間
在區間![]() 上的單調性.
上的單調性.
科目:高中數學 來源: 題型:
【題目】甲乙兩人進行圍棋比賽,約定先連勝兩局者直接贏得比賽,若賽完5局仍未出現連勝,則判定獲勝局數多者贏得比賽,假設每局甲獲勝的概率為![]() ,乙獲勝的概率為
,乙獲勝的概率為![]() ,各局比賽結果相互獨立.
,各局比賽結果相互獨立.
求甲在4局以內(含4局)贏得比賽的概率;
記![]() 為比賽決出勝負時的總局數,求
為比賽決出勝負時的總局數,求![]() 的分布列和均值(數學期望).
的分布列和均值(數學期望).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高校甲、乙、丙、丁四個專業分別有150,150,400,300名學生.為了解學生的就業傾向,用分層抽樣的方法從該校這四個專業中抽取60名學生進行調查,則應從丁專業抽取的學生人數為____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,有一張半徑為1米的圓形鐵皮,工人師傅需要剪一塊頂角為銳角的等腰三角形![]() ,不妨設
,不妨設 ![]() ,
, ![]() 邊上的高為
邊上的高為 ![]() ,圓心為
,圓心為 ![]() ,為了使三角形的面積最大,我們設計了兩種方案.
,為了使三角形的面積最大,我們設計了兩種方案.

(1)方案1:設 ![]() 為
為 ![]() ,用
,用![]() 表示
表示 ![]() 的面積
的面積 ![]() ; 方案2:設
; 方案2:設![]() 的高
的高![]() 為
為![]() ,用
,用![]() 表示
表示 ![]() 的面積
的面積![]() ;
;
(2)請從(1)中的兩種方案中選擇一種,求出![]() 面積的最大值
面積的最大值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱ABC—A1B1C1中,BC=3,AB=4,AC=CC1=5,M,N分別是A1B,B1C1的中點.
(1)求證:MN//平面ACC1A1;
(2)求點N到平面MBC的距離.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐P-ABC中,![]() 底面ABC,
底面ABC,![]() .點D,E,N分別為棱PA,PC,BC的中點,M是線段AD的中點,
.點D,E,N分別為棱PA,PC,BC的中點,M是線段AD的中點,![]() ,
,![]() .
.
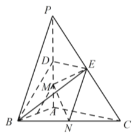
(1)求證:![]() 平面BDE;
平面BDE;
(2)求二面角C-EM-N的正弦值.
(3)已知點H在棱PA上,且直線NH與直線BE所成角的余弦值為![]() ,求線段AH的長.
,求線段AH的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com