
| A. | (2,+∞) | B. | (0,1) | C. | (1,+∞) | D. | (0,ln2) |
分析 構造函數g(x)=$\frac{f(x)}{{e}^{x}}$,利用導數可判斷g(x)的單調性,再根據f(ln2)=2,求得g(ln2)=1,繼而求出答案
解答 解:∵?x∈R,都有f′(x)>f(x)成立,
∴f′(x)-f(x)>0,于是有( $\frac{f(x)}{{e}^{x}}$)′>0,
令g(x)=$\frac{f(x)}{{e}^{x}}$,則有g(x)在R上單調遞增,
∵不等式f(x)>ex,
∴g(x)>1,
∵f(2)=e2,
∴g(2)=$\frac{f(2)}{{e}^{2}}$=1,
∴x>2,
故選:A.
點評 本題考查導數的運算及利用導數研究函數的單調性,屬中檔題,解決本題的關鍵是根據選項及已知條件合理構造函數,利用導數判斷函數的單調性.


科目:高中數學 來源: 題型:解答題
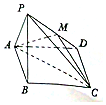 如圖,已知四棱錐P-ABCD中,底面ABCD為菱形,且∠DAB=60°,△PAB是邊長為a的正三角形,且平面PAB⊥平面ABCD,已知點M是PD的中點.
如圖,已知四棱錐P-ABCD中,底面ABCD為菱形,且∠DAB=60°,△PAB是邊長為a的正三角形,且平面PAB⊥平面ABCD,已知點M是PD的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
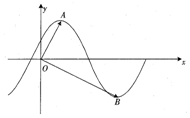 已知函數f(x)=Msin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分圖象如下圖所示,其中A,B分別為函數f(x)圖象的一個最高點和最低點,且A,B兩點的橫坐標分別為1,4,若$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,則函數f(x)的一個單調減區間為( )
已知函數f(x)=Msin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分圖象如下圖所示,其中A,B分別為函數f(x)圖象的一個最高點和最低點,且A,B兩點的橫坐標分別為1,4,若$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,則函數f(x)的一個單調減區間為( )| A. | (-6,-3) | B. | (6,9) | C. | (7,10) | D. | (10,13) |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
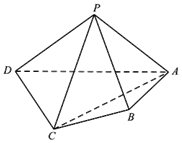 如圖,在四棱錐P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.
如圖,在四棱錐P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
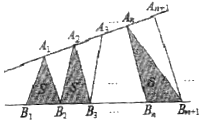 如圖,點列{An},{Bn}分別在某個銳角的兩邊上,且|AnAn+1|=|An+1An+2|,An≠An+2,n∈N*,|BnBn+1|=|Bn+1Bn+2|,Bn≠Bn+2,n∈N*(P≠Q表示P與Q不重合).若dn=|AnBn|,Sn為△AnBnBn+1的面積,則( )
如圖,點列{An},{Bn}分別在某個銳角的兩邊上,且|AnAn+1|=|An+1An+2|,An≠An+2,n∈N*,|BnBn+1|=|Bn+1Bn+2|,Bn≠Bn+2,n∈N*(P≠Q表示P與Q不重合).若dn=|AnBn|,Sn為△AnBnBn+1的面積,則( )| A. | {dn}是等差數列 | B. | {dn2}是等差數列 | C. | {Sn}是等差數列 | D. | {Sn2}是等差數列 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com