
【題目】已知函數f(x)=2x3﹣3ax2+1.
(1)若a=﹣1,求函數f(x)的單調區間;
(2)若函數f(x)有且只有2個不同的零點,求實數a的值;
(3)若函數y=|f(x)|在[0,1]上的最小值是0,求實數a的取值范圍.
【答案】(1)函數f(x)的增區間為(﹣∞,﹣1),(0,+∞),減區間為(﹣1,0)
(2)1
(3)[1,+∞)
【解析】
(1)求出![]() 的導數,解關于導函數的不等式,求出函數的單調區間即可;
的導數,解關于導函數的不等式,求出函數的單調區間即可;
(2)通過討論![]() 的范圍,確定函數的單調性, 函數
的范圍,確定函數的單調性, 函數![]() 有且只有
有且只有![]() 個不同的零點即可求得
個不同的零點即可求得![]() 的值;
的值;
(3)通過討論![]() 的范圍,確定函數的單調性,再根據函數
的范圍,確定函數的單調性,再根據函數![]() 在
在![]() 上的最小值是
上的最小值是![]() 并結合圖像可求得實數
并結合圖像可求得實數![]() 的取值范圍.
的取值范圍.
(1)![]() 時,
時,![]() .
.
![]() 當
當![]() ,
,![]() 時,
時,
![]() ,
,
當![]() 時,
時,![]() ,
,
故函數![]() 的增區間為
的增區間為![]() ,
,![]() ,減區間為
,減區間為![]() .
.
(2)![]() ,
,![]()
①![]() 時,
時,![]() 在
在![]() 上單調遞增,不存在兩個零點;
上單調遞增,不存在兩個零點;
②![]() 時,
時,![]() 在
在![]() ,
,![]() 遞增,在
遞增,在![]() 遞減.
遞減.
其圖象如下:
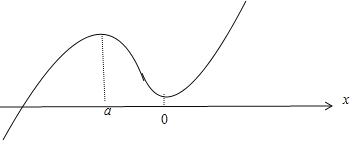
函數![]() 不存在2個不同的零點;
不存在2個不同的零點;
③![]() 時,
時,![]() 在
在![]() ,
,![]() 遞增,在
遞增,在![]() 遞減.
遞減.
其圖象如下:
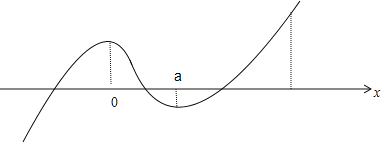
![]() 只需
只需![]() ,
,![]() 即可
即可
綜上,函數![]() 有且只有
有且只有![]() 個不同的零點,實數
個不同的零點,實數![]() 的值為
的值為![]() .
.
(3)①![]() 時,
時,![]() 在
在![]() 上單調遞增,
上單調遞增,![]() ,不符合題意;
,不符合題意;
②![]() 時,
時,![]() 在
在![]() 遞增,
遞增,![]() ,不符合題意;
,不符合題意;
③![]() 時,
時,![]() 在
在![]() ,
,![]() 遞增,在
遞增,在![]() 遞減.
遞減.
![]() 圖象如下:
圖象如下:

要使函數![]() 在
在![]() 上的最小值是
上的最小值是![]() ,只需
,只需![]() ,
,![]() ,
,
故實數![]() 的取值范圍為
的取值范圍為![]() .
.


 名校名師培優作業本加核心試卷系列答案
名校名師培優作業本加核心試卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中數學 來源: 題型:
【題目】給出以下四個命題:
(1)命題![]() ,使得
,使得![]() ,則
,則![]() ,都有
,都有![]() ;
;
(2)已知函數f(x)=|log2x|,若a≠b,且f(a)=f(b),則ab=1;
(3)若平面α內存在不共線的三點到平面β的距離相等,則平面α平行于平面β;
(4)已知定義在![]() 上的函數
上的函數![]() 滿足條件
滿足條件![]() ,且函數
,且函數![]() 為奇函數,則函數
為奇函數,則函數![]() 的圖象關于點
的圖象關于點![]() 對稱.
對稱.
其中真命題的序號為______________.(寫出所有真命題的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某花圃為提高某品種花苗質量,開展技術創新活動,在![]() 實驗地分別用甲、乙方法培訓該品種花苗.為觀測其生長情況,分別在實驗地隨機抽取各
實驗地分別用甲、乙方法培訓該品種花苗.為觀測其生長情況,分別在實驗地隨機抽取各![]() 株,對每株進行綜合評分,將每株所得的綜合評分制成如圖所示的頻率分布直方圖.記綜合評分為
株,對每株進行綜合評分,將每株所得的綜合評分制成如圖所示的頻率分布直方圖.記綜合評分為![]() 及以上的花苗為優質花苗.
及以上的花苗為優質花苗.

![]() 求圖中
求圖中![]() 的值,并求綜合評分的中位數.
的值,并求綜合評分的中位數.
![]() 用樣本估計總體,以頻率作為概率,若在
用樣本估計總體,以頻率作為概率,若在![]() 兩塊試驗地隨機抽取
兩塊試驗地隨機抽取![]() 棵花苗,求所抽取的花苗中的優質花苗數的分布列和數學期望;
棵花苗,求所抽取的花苗中的優質花苗數的分布列和數學期望;
![]() 填寫下面的列聯表,并判斷是否有
填寫下面的列聯表,并判斷是否有![]() 的把握認為優質花苗與培育方法有關.
的把握認為優質花苗與培育方法有關.
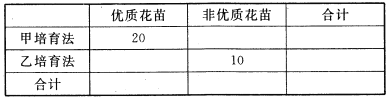
附:下面的臨界值表僅供參考.
![]()
(參考公式:![]() ,其中
,其中![]() .)
.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() 為
為![]() 邊上一點,
邊上一點,![]() ,
,![]() .
.
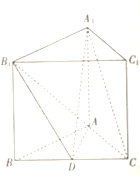
(1)證明:平面![]() 平面
平面![]() .
.
(2)若![]() ,試問:
,試問:![]() 是否與平面
是否與平面![]() 平行?若平行,求三棱錐
平行?若平行,求三棱錐![]() 的體積;若不平行,請說明理由.
的體積;若不平行,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
(1)證明:數列![]() 是等比數列,并求數列
是等比數列,并求數列![]() 的通項公式;
的通項公式;
(2)在數列![]() 中,是否存在連續三項成等差數列?若存在,求出所有符合條件的項;若不存在,請說明理由;
中,是否存在連續三項成等差數列?若存在,求出所有符合條件的項;若不存在,請說明理由;
(3)若![]() 且
且![]() ,
,![]() ,求證:使得
,求證:使得![]() ,
,![]() ,
,![]() 成等差數列的點列
成等差數列的點列![]() 在某一直線上.
在某一直線上.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直三棱柱ABC-A1B1C1中,底面△ABC是直角三角形,AC=BC=AA1=2,D為側棱AA1的中點.
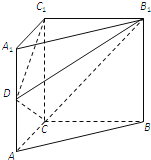
(1)求異面直線DC1,B1C所成角的余弦值;
(2)求二面角B1-DC-C1的平面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠共有男女員工500人,現從中抽取100位員工對他們每月完成合格產品的件數統計如下:
每月完成合格產品的件數(單位:百件) |
|
|
|
|
|
頻數 | 10 | 45 | 35 | 6 | 4 |
男員工人數 | 7 | 23 | 18 | 1 | 1 |
(1)其中每月完成合格產品的件數不少于3200件的員工被評為“生產能手”.由以上統計數據填寫下面![]() 列聯表,并判斷是否有95%的把握認為“生產能手”與性別有關?
列聯表,并判斷是否有95%的把握認為“生產能手”與性別有關?
非“生產能手” | “生產能手” | 合計 | |
男員工 | |||
女員工 | |||
合計 |
(2)為提高員工勞動的積極性,工廠實行累進計件工資制:規定每月完成合格產品的件數在定額2600件以內的,計件單價為1元;超出![]() 件的部分,累進計件單價為1.2元;超出
件的部分,累進計件單價為1.2元;超出![]() 件的部分,累進計件單價為1.3元;超出400件以上的部分,累進計件單價為1.4元.將這4段中各段的頻率視為相應的概率,在該廠男員工中選取1人,女員工中隨機選取2人進行工資調查,設實得計件工資(實得計件工資=定額計件工資+超定額計件工資)不少于3100元的人數為,求的分布列和數學期望.
件的部分,累進計件單價為1.3元;超出400件以上的部分,累進計件單價為1.4元.將這4段中各段的頻率視為相應的概率,在該廠男員工中選取1人,女員工中隨機選取2人進行工資調查,設實得計件工資(實得計件工資=定額計件工資+超定額計件工資)不少于3100元的人數為,求的分布列和數學期望.
附:![]() ,
,
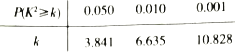 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com