
【題目】在直三棱柱ABC-A1B1C1中,底面△ABC是直角三角形,AC=BC=AA1=2,D為側棱AA1的中點.
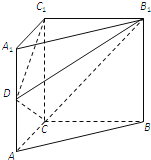
(1)求異面直線DC1,B1C所成角的余弦值;
(2)求二面角B1-DC-C1的平面角的余弦值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)以C為原點,CA、CB、CC1為坐標軸,建立空間直角坐標系C﹣xyz,寫出要用的點的坐標,寫出兩個向量的方向向量,根據兩個向量所成的角得到兩條異面直線所成的角.
(2)先求兩個平面的法向量,在第一問的基礎上,有一個平面的法向量是已知的,只要寫出向量的表示形式就可以,另一個平面的向量需要求出,根據兩個法向量所成的角得到結果.
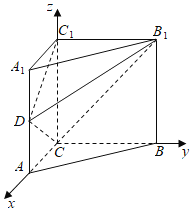
(1)如圖所示,以C為原點,CA、CB、CC1為坐標軸,建立空間直角坐標系
C﹣xyz.
則C(0,0,0),A(2,0,0),B(0,2,0),C1(0,0,2),B1(0,2,2),D(2,0,1).
所以![]() (﹣2,0,1),
(﹣2,0,1),![]() (0,﹣2,﹣2).
(0,﹣2,﹣2).
所以cos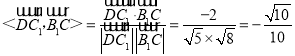 .
.
即異面直線DC1與B1C所成角的余弦值為![]() .
.
(2)因為![]() (0,2,0),
(0,2,0),![]() (2,0,0),
(2,0,0),![]() (0,0,2),
(0,0,2),
所以![]()
![]() 0,
0,![]()
![]() 0,
0,
所以![]() 為平面ACC1A1的一個法向量.
為平面ACC1A1的一個法向量.
因為![]() (0,﹣2,﹣2),
(0,﹣2,﹣2),![]() (2,0,1),
(2,0,1),
設平面B1DC的一個法向量為n,n=(x,y,z).
由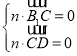 ,得
,得![]()
令/span>x=1,則y=2,z=﹣2,n=(1,2,﹣2).
所以cos<n, .
.
所以二面角B1﹣DC﹣C1的余弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】
在平面直角坐標系中,以坐標原點為極點,x軸的非負半軸為極軸建立極坐標系.已知點A的極坐標(![]() ,
,![]() ),直線l的極坐標方程為ρcos(θ-
),直線l的極坐標方程為ρcos(θ-![]() )=a,.
)=a,.
(1)若點A在直線l上,求直線l的直角坐標方程;
(2)圓C的參數方程為![]() (
(![]() 為參數),若直線
為參數),若直線![]() 與圓C相交的弦長為
與圓C相交的弦長為![]() ,求
,求![]() 的值。
的值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】汽車的“燃油效率”是指汽車每消耗1升汽油行駛的里程,下圖描述了甲、乙、丙三輛汽車在不同速度下的燃油效率情況. 下列敘述中正確的是( )

A. 消耗1升汽油,乙車最多可行駛5千米
B. 以相同速度行駛相同路程,三輛車中,甲車消耗汽油最多
C. 甲車以80千米/小時的速度行駛1小時,消耗10升汽油
D. 某城市機動車最高限速80千米/小時. 相同條件下,在該市用丙車比用乙車更省油
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其最小正周期為
,其最小正周期為 ![]() .
.
(1)求 ![]() 的表達式;
的表達式;
(2)將函數![]() 的圖象向右平移
的圖象向右平移![]() 個單位長度后,再將得到的圖象上各點的橫坐標伸長到原來的
個單位長度后,再將得到的圖象上各點的橫坐標伸長到原來的![]() 倍(縱坐標不變),得到函數
倍(縱坐標不變),得到函數 ![]() 的圖象,若關于
的圖象,若關于 ![]() 的方程
的方程 ![]() 在區間
在區間 ![]() 上有解,求實數
上有解,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年8月18日,舉世矚目的第18屆亞運會在印尼首都雅加達舉行,為了豐富亞運會志愿者的業余生活,同時鼓勵更多的有志青年加入志愿者行列,大會主辦方決定對150名志愿者組織一次有關體育運動的知識競賽(滿分120分)并計劃對成績前15名的志愿者進行獎勵,現將所有志愿者的競賽成績制成頻率分布直方圖,如圖所示,若第三組與第五組的頻數之和是第二組的頻數的3倍,試回答以下問題:

(1)求圖中![]() 的值;
的值;
(2)求志愿者知識競賽的平均成績;
(3)從受獎勵的15人中按成績利用分層抽樣抽取5人,再從抽取的5人中,隨機抽取2人在主會場服務,求抽取的這2人中其中一人成績在![]() 分的概率.
分的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com