
若數列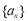 的各項均為正數,
的各項均為正數,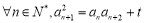 ,
, 為常數,且
為常數,且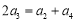 .
.
(1)求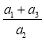 的值;
的值;
(2)證明:數列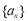 為等差數列;
為等差數列;
(3)若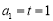 ,對任意給定的k∈N*,是否存在p,r∈N*(k<p<r)使
,對任意給定的k∈N*,是否存在p,r∈N*(k<p<r)使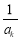 ,
,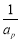 ,
,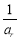 成等差數列?若存在,用k分別表示一組p和r;若不存在,請說明理由.
成等差數列?若存在,用k分別表示一組p和r;若不存在,請說明理由.
(1)2(2)詳見解析(3)當k=1時,不存在p,r;當k≥2時,存在一組p=2k-1,r=k(2k-1)滿足題意.
【解析】
試題分析:(1)令 ,得
,得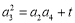 ①,令
①,令 ,得
,得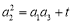 ②,①—②,得
②,①—②,得 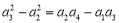 ,
, 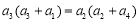 ,
, (2)證明數列為等差數列,一般利用定義進行證明,由(1)推導過程知:
(2)證明數列為等差數列,一般利用定義進行證明,由(1)推導過程知: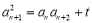 ,
, 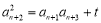 ,兩式相減得
,兩式相減得 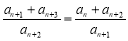
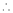 數列
數列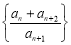 為常數數列,
為常數數列,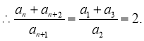
 ,
,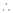 數列
數列 為等差數列(3)先求數列
為等差數列(3)先求數列 通項公式:由(2)知,數列
通項公式:由(2)知,數列 為等差數列,設公差為
為等差數列,設公差為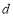 ,則由條件
,則由條件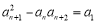 ,得
,得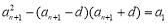
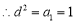 ,又數列
,又數列 的各項為正數,
的各項為正數,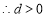 ,
,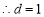 ,
,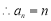
若存在p,r使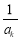 ,
,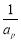 ,
,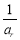 成等差數列,則
成等差數列,則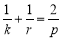 所以
所以 ;當k=1時,
;當k=1時,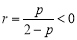 ,舍去;當k≥2時,令p=2k-1得r=kp=k(2k-1),滿足k<p<r.
,舍去;當k≥2時,令p=2k-1得r=kp=k(2k-1),滿足k<p<r.
試題解析:【解析】
(1)由條件,設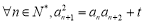
令 ,得
,得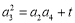 ①,令
①,令 ,得
,得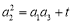 ②
②
①—②,得 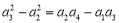 ,
, 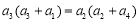 ,
,
 4分
4分
(2)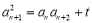 ,
, 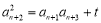 ,
,
兩式相減得 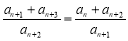 7分
7分
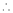 數列
數列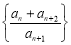 為常數數列,
為常數數列,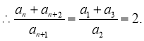
 ,
, 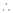 數列
數列 為等差數列. 10分
為等差數列. 10分
(3)由(2)知,數列 為等差數列,設公差為
為等差數列,設公差為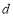 ,
,
則由條件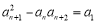 ,得
,得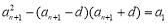
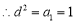 ,又數列
,又數列 的各項為正數,
的各項為正數,
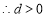 ,
,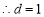 ,
,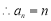 . 12分
. 12分
當k=1時,若存在p,r使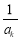 ,
,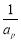 ,
,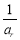 成等差數列,則
成等差數列,則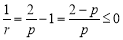
與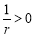 矛盾.因此,當k=1時,不存在. 14分
矛盾.因此,當k=1時,不存在. 14分
當k≥2時,則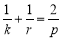 所以
所以
令p=2k-1得r=kp=k(2k-1),滿足k<p<r.
綜上所述,當k=1時,不存在p,r;
當k≥2時,存在一組p=2k-1,r=k(2k-1)滿足題意. 16分
考點:等差數列


科目:高中數學 來源:2014-2015學年黑龍江省綏化市三校高二上學期期中聯考數學試卷(解析版) 題型:選擇題
函數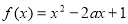 在
在 上是單調遞減函數的必要不充分條件是( )
上是單調遞減函數的必要不充分條件是( )
A. B.
B. C.
C. D.
D.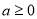
查看答案和解析>>
科目:高中數學 來源:2014-2015學年江蘇省等五校高三12月第一次聯考理科數學試卷(解析版) 題型:解答題
(本小題滿分10分)袋中裝有大小相同的黑球和白球共9個,從中任取2個都是白球的概率為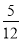 .現甲、乙兩人從袋中輪流摸球,甲先取,乙后取,然后甲再取 ,每次摸取1個球,取出的球不放回,直到其中有一人取到白球時終止.用X表示取球終止時取球的總次數.
.現甲、乙兩人從袋中輪流摸球,甲先取,乙后取,然后甲再取 ,每次摸取1個球,取出的球不放回,直到其中有一人取到白球時終止.用X表示取球終止時取球的總次數.
(1)求袋中原有白球的個數;
(2)求隨機變量X的概率分布及數學期望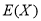 .
.
查看答案和解析>>
科目:高中數學 來源:2014-2015學年江蘇省等五校高三12月第一次聯考理科數學試卷(解析版) 題型:解答題
已知函數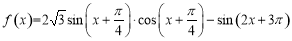 .
.
(1)求 的最小正周期;
的最小正周期;
(2)若將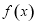 的圖像向左平移
的圖像向左平移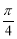 個單位,得到函數
個單位,得到函數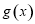 的圖像,求函數
的圖像,求函數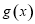 在區間
在區間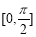 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源:2014-2015學年江蘇省等五校高三12月第一次聯考理科數學試卷(解析版) 題型:填空題
設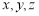 是空間的不同直線或不同平面,下列條件中能保證“若
是空間的不同直線或不同平面,下列條件中能保證“若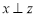 ,且
,且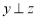 ,則
,則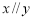 ”為真命題的是 . (填所正確條件的代號)
”為真命題的是 . (填所正確條件的代號)
①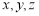 為直線;
為直線;
②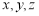 為平面;
為平面;
③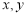 為直線,
為直線,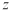 為平面;
為平面;
④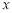 為直線,
為直線,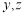 為平面.
為平面.
查看答案和解析>>
科目:高中數學 來源:2015屆江蘇教育學院附屬高中高三上學期期中文科數學試卷(解析版) 題型:填空題
定義在(-1,1)上的函數f(x)=-3x+sinx,如果f(1-a)+f(1-a2)>0,則實數 的取值范圍為 .
的取值范圍為 .
查看答案和解析>>
科目:高中數學 來源:2014-2015學年浙江省嘉興市高三新高考單科綜合調研三文科數學試卷(解析版) 題型:填空題
已知平行四邊形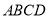 中,
中,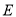 為
為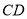 的中點,
的中點,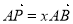 ,
,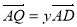 ,其中
,其中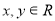 ,且均不為0,若
,且均不為0,若 ,則
,則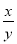 = .
= .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com