
【題目】已知無窮數列![]() 的各項均為正數,其前
的各項均為正數,其前![]() 項和為
項和為![]() ,
, ![]() .
.
(1)如果![]() ,且對于一切正整數
,且對于一切正整數![]() ,均有
,均有![]() ,求
,求![]() ;
;
(2)如果對于一切正整數![]() ,均有
,均有![]() ,求
,求![]() ;
;
(3)如果對于一切正整數![]() ,均有
,均有![]() ,證明:
,證明: ![]() 能被8整除.
能被8整除.
【答案】(1) ![]() ;(2)
;(2) 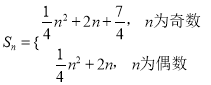 . (3) 見解析.
. (3) 見解析.
【解析】試題分析:(1)由![]() ,得
,得![]() ,根據等比數列的通項公式得到通項;(2)推導出an+1﹣an﹣1=1.a1=4,由anan+1=Sn,得a2=1,a3=5,a4=3,…,由此根據n為偶數和n為奇數,能求出Sn的值;(3)推導出
,根據等比數列的通項公式得到通項;(2)推導出an+1﹣an﹣1=1.a1=4,由anan+1=Sn,得a2=1,a3=5,a4=3,…,由此根據n為偶數和n為奇數,能求出Sn的值;(3)推導出![]() ,分別求出前4項的值,利用數學歸納法能證明a3n﹣1能被8整除.
,分別求出前4項的值,利用數學歸納法能證明a3n﹣1能被8整除.
解析:
(1) 數列![]() 的各項均為正數,由
的各項均為正數,由![]() ,得
,得![]() ,
,
![]() 數列
數列![]() 是等比數列,公比
是等比數列,公比![]() ,從而
,從而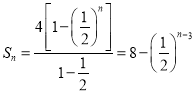
(2) 由![]() 得
得![]() ,兩式相減得
,兩式相減得![]() ,
,
![]() 此數列各均為正數,
此數列各均為正數, ![]()
![]() ,
, ![]() 數列
數列![]() 和數列
和數列![]() 均是公差為1的等差數列.由
均是公差為1的等差數列.由![]() ,得
,得![]() .
.
當![]() 為偶數時,
為偶數時, ![]()
![]()
當![]() 為奇數時,
為奇數時, ![]()
![]()
 .
.
(3) 由![]() 得
得![]() ,兩式相減得
,兩式相減得![]() .
.
![]()
![]() ,得
,得![]() ,
, ![]() .
. ![]()
以下證明:對于![]() ,
, ![]() 被8除余數為4,
被8除余數為4, ![]() 被8整除,
被8整除, ![]() 被8除余數為4.
被8除余數為4.
當![]() 時,
時, ![]() ,
, ![]() ,
, ![]() ,命題正確.
,命題正確.
假設![]() 時,命題正確,即
時,命題正確,即![]() ,
, ![]() ,
, ![]() 其中
其中![]() ,
, ![]() .
.
那么, ![]() ,
, ![]()
![]() 為正整數,
為正整數, ![]()
![]() 被8除余數為4.
被8除余數為4.
![]() .
.
![]()
![]() 為正整數,
為正整數, ![]()
![]() 能被8整除.
能被8整除.
![]()
![]() .
. ![]()
![]() 為正整數,
為正整數, ![]()
![]() 被8除余數為4.
被8除余數為4.
即![]() 時,命題也正確.
時,命題也正確.
從而證得,對于一切正整數![]() ,
, ![]() 能被8整除.
能被8整除.


 輕松奪冠全能掌控卷系列答案
輕松奪冠全能掌控卷系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知直線![]() 與圓O:
與圓O:![]() 相切.
相切.
(1)直線l過點(2,1)且截圓O所得的弦長為![]() ,求直線l的方程;
,求直線l的方程;
(2)已知直線y=3與圓O交于A,B兩點,P是圓上異于A,B的任意一點,且直線AP,BP與y軸相交于M,N點.判斷點M、N的縱坐標之積是否為定值?若是,求出該定值;若不是,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高一舉行了一次數學競賽,為了了解本次競賽學生的成績情況,從中抽取了部分學生的分數(得分取正整數,滿分為![]() )作為樣本(樣本容量
)作為樣本(樣本容量![]() )進行統計,按照
)進行統計,按照![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 的分組作出頻率分布直方圖,已知得分在
的分組作出頻率分布直方圖,已知得分在![]() 、
、![]() 的頻數分別為
的頻數分別為![]() 、
、![]() .
.
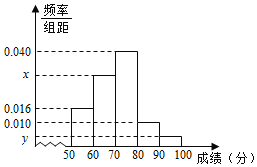
(1)求樣本容量![]() 和頻率分布直方圖中的
和頻率分布直方圖中的![]() 、
、![]() 的值;
的值;
(2)估計本次競賽學生成績的眾數、中位數、平均數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學高二年級組織外出參加學業水平考試,出行方式為:乘坐學校定制公交或自行打車前往,大數據分析顯示,當![]() 的學生選擇自行打車,自行打車的平均時間為
的學生選擇自行打車,自行打車的平均時間為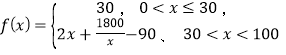 (單位:分鐘) ,而乘坐定制公交的平均時間不受
(單位:分鐘) ,而乘坐定制公交的平均時間不受![]() 影響,恒為40分鐘,試根據上述分析結果回答下列問題:
影響,恒為40分鐘,試根據上述分析結果回答下列問題:
(1)當![]() 在什么范圍內時,乘坐定制公交的平均時間少于自行打車的平均時間?
在什么范圍內時,乘坐定制公交的平均時間少于自行打車的平均時間?
(2)求該校學生參加考試平均時間![]() 的表達式:討論
的表達式:討論![]() 的單調性,并說明其實際意義.
的單調性,并說明其實際意義.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某動物園要為剛入園的小動物建造一間兩面靠墻的三角形露天活動室,地面形狀如圖所示,已知已有兩面墻的夾角為![]() ,墻
,墻![]() 的長度為
的長度為![]() 米,(已有兩面墻的可利用長度足夠大),記
米,(已有兩面墻的可利用長度足夠大),記![]() .
.
(1)若![]() ,求
,求![]() 的周長(結果精確到0.01米);
的周長(結果精確到0.01米);
(2)為了使小動物能健康成長,要求所建的三角形露天活動室面積,![]() 的面積盡可能大,當
的面積盡可能大,當![]() 為何值時,該活動室面積最大?并求出最大面積.
為何值時,該活動室面積最大?并求出最大面積.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校從參加高三模擬考試的學生中隨機抽取60名學生,將其數學成績(均為整數)分成六組[90,100),[100,110),…,[140,150]后得到如下部分頻率分布直方圖,觀察圖形的信息,回答下列問題:
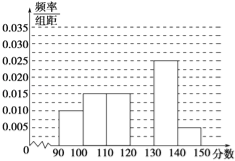
(1)求分數在[120,130)內的頻率;
(2)若在同一組數據中,將該組區間的中點值(如:組區間[100,110)的中點值為![]() =105)作為這組數據的平均分,據此,估計本次考試的平均分;
=105)作為這組數據的平均分,據此,估計本次考試的平均分;
(3)用分層抽樣的方法在分數段為[110,130)的學生中抽取一個容量為6的樣本,將該樣本看成一個總體,從中任取2人,求至多有1人在分數段[120,130)內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,動點
中,動點![]() 到定點
到定點![]() 的距離與它到直線
的距離與它到直線![]() 的距離相等.
的距離相等.
(1)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)設動直線![]() 與曲線
與曲線![]() 相切于點
相切于點![]() ,與直線
,與直線![]() 相交于點
相交于點![]() .
.
證明:以![]() 為直徑的圓恒過
為直徑的圓恒過![]() 軸上某定點.
軸上某定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓M:![]() ,直線l:
,直線l:![]() ,下列四個選項,其中正確的是( )
,下列四個選項,其中正確的是( )
A.對任意實數k與θ,直線l和圓M有公共點
B.存在實數k與θ,直線l和圓M相離
C.對任意實數k,必存在實數θ,使得直線l與圓M相切
D.對任意實數θ,必存在實數k,使得直線l與圓M相切
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com