
【題目】如圖,在四棱錐![]() 中,側面
中,側面![]() 底面
底面![]() ,底面
,底面![]() 為矩形,
為矩形, ![]() 為
為![]() 中點,
中點, ![]() ,
, ![]() ,
, ![]() .
.

(Ⅰ)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)證明見解析;(Ⅱ) ![]() .
.
【解析】試題分析:(Ⅰ)設![]() 與
與![]() 的交點為
的交點為![]() ,連結
,連結![]() ,則
,則![]() 為
為![]() 的中點,由
的中點,由![]() 為
為![]() 中點,利用三角形中位線定理可得
中點,利用三角形中位線定理可得![]() ,從而根據線面平行的判定定理可得
,從而根據線面平行的判定定理可得![]() 平面
平面![]() ;(Ⅱ)由勾股定理可得
;(Ⅱ)由勾股定理可得![]() ,根據線面垂直的性質定理得
,根據線面垂直的性質定理得![]() 平面
平面![]() ,故
,故![]() ,再根據線面垂直的判定定理可得
,再根據線面垂直的判定定理可得![]() 平面
平面![]() ,故
,故![]() 就是直線
就是直線![]() 與平面
與平面![]() 所成的角,在直角
所成的角,在直角![]() 中可得
中可得![]() .
.
試題解析:
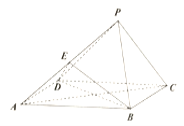
(Ⅰ)設![]() 與
與![]() 的交點為
的交點為![]() ,連結
,連結![]() .
.
因為![]() 為矩形,所以
為矩形,所以![]() 為
為![]() 的中點.
的中點.
在![]() 中,由已知
中,由已知![]() 為
為![]() 中點,所以
中點,所以![]() .
.
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)在![]() 中,
中, ![]() ,
, ![]() ,
,
所以![]() ,
,
即![]() .
.
因為平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
, ![]() ,
,
所以![]() 平面
平面![]() ,故
,故![]() .
.
又因為![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
故![]() 就是直線
就是直線![]() 與平面
與平面![]() 所成的角.
所成的角.
在直角![]() 中
中![]() ,
, ![]() ,
,
所以![]() .
.
即直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.
【方法點晴】本題主要考查線面平行的判定定理、直線和平面成的角的定義及求法,屬于難題. 證明線面平行的常用方法:①利用線面平行的判定定理,使用這個定理的關鍵是設法在平面內找到一條與已知直線平行的直線,可利用幾何體的特征,合理利用中位線定理、線面平行的性質或者構造平行四邊形、尋找比例式證明兩直線平行.②利用面面平行的性質,即兩平面平行,在其中一平面內的直線平行于另一平面. 本題(1)是就是利用方法①證明的.


科目:高中數學 來源: 題型:
【題目】十九大指出中國的電動汽車革命早已展開,通過以新能源汽車替代汽/柴油車,中國正在大力實施一項將重塑全球汽車行業的計劃.2018年某企業計劃引進新能源汽車生產設備,通過市場分析,全年需投入固定成本2500萬元,每生產x(百輛),需另投入成本![]() 萬元,且
萬元,且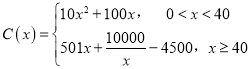 .由市場調研知,每輛車售價5萬元,且全年內生產的車輛當年能全部銷售完.
.由市場調研知,每輛車售價5萬元,且全年內生產的車輛當年能全部銷售完.
(1)求出2018年的利潤L(x)(萬元)關于年產量x(百輛)的函數關系式;(利潤=銷售額-成本)
(2)2018年產量為多少百輛時,企業所獲利潤最大?并求出最大利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,拋物線![]() 的焦點為
的焦點為![]() ,拋物線上一定點
,拋物線上一定點![]() .
.
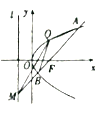
(1)求拋物線![]() 的方程及準線
的方程及準線![]() 的方程;
的方程;
(2)過焦點![]() 的直線(不經過
的直線(不經過![]() 點)與拋物線交于
點)與拋物線交于![]() 兩點,與準線
兩點,與準線![]() 交于點
交于點![]() ,記
,記![]() 的斜率分別為
的斜率分別為![]() ,問是否存在常數
,問是否存在常數![]() ,使得
,使得![]() 成立?若存在
成立?若存在![]() ,求出
,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[2018·贛中聯考]李冶(1192-1279),真實欒城(今屬河北石家莊市)人,金元時期的數學家、詩人,晚年在封龍山隱居講學,數學著作多部,其中《益古演段》主要研究平面圖形問題:求圓的直徑、正方形的邊長等.其中一問:現有正方形方田一塊,內部有一個圓形水池,其中水池的邊緣與方田四邊之間的面積為13.75畝,若方田的四邊到水池的最近距離均為二十步,則圓池直徑和方田的邊長分別是(注:240平方步為1畝,圓周率按3近似計算)( )
A. 10步,50步 B. 20步,60步 C. 30步,70步 D. 40步,80步
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著共享單車的成功運營,更多的共享產品逐步走入大家的世界,共享汽車、共享籃球、共享充電寶等各種共享產品層出不窮.某公司隨即抽取![]() 人對共享產品是否對日常生活有益進行了問卷調查,并對參與調查的
人對共享產品是否對日常生活有益進行了問卷調查,并對參與調查的![]() 人中的性別以及意見進行了分類,得到的數據如下表所示:
人中的性別以及意見進行了分類,得到的數據如下表所示:
男 | 女 | 總計 | |
認為共享產品對生活有益 |
|
|
|
認為共享產品對生活無益 |
|
|
|
總計 |
|
|
|
(1)根據表中的數據,能否在犯錯誤的概率不超過![]() 的前提下,認為對共享產品的態度與性別有關系?
的前提下,認為對共享產品的態度與性別有關系?
(2)現按照分層抽樣從認為共享產品增多對生活無益的人員中隨機抽取![]() 人,再從
人,再從![]() 人中隨機抽取
人中隨機抽取![]() 人贈送超市購物券作為答謝,求恰有
人贈送超市購物券作為答謝,求恰有![]() 人是女性的概率.
人是女性的概率.
參與公式: 
臨界值表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() (實數
(實數![]() 為常數)
為常數)
(1)當![]() 時,證明
時,證明![]() 在
在![]() 上單調遞減;
上單調遞減;
(2)若![]() ,且
,且![]() 為偶函數,求實數
為偶函數,求實數![]() 的值;
的值;
(3)小金同學在求解函數![]() 的對稱中心時,發現函數
的對稱中心時,發現函數![]() 是一個復合函數,設
是一個復合函數,設![]() ,
,![]() ,則
,則![]() ,顯然
,顯然![]() 有對稱中心,設為
有對稱中心,設為![]() ,
,![]() 有反函數
有反函數![]() ,則
,則![]() 的對稱中心為
的對稱中心為![]() ,請問小金的做法是否正確?如果正確,請給出證明,并直接寫出當
,請問小金的做法是否正確?如果正確,請給出證明,并直接寫出當![]() 時
時![]() 的對稱中心;如果錯誤,請舉出反例,并用正確的方法直接寫出當
的對稱中心;如果錯誤,請舉出反例,并用正確的方法直接寫出當![]() 時
時![]() 的對稱中心.
的對稱中心.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com