
分析 通過記遞增的等差數列{an}的公差為d(d>0),利用a1,a2,a4成等比數列可知公差d=1,進而可知數列{an}是首項、公差均為1的等差數列,再由數列{a4n+4}是首項為4、公差為4的等差數列,運用求和公式計算即得結論.
解答 解:記遞增的等差數列{an}的公差為d(d>0),
由a1=1可知,a2=1+d,a4=1+3d,
又∵a1,a2,a4成等比數列,
∴a22=a1a4,即(1+d)2=1+3d,
整理得:d2=d,
解得:d=1或d=0(舍),
∴數列{an}是首項、公差均為1的等差數列,
∴an=n,
∴數列{a4n+4}是首項為4、公差為4的等差數列,
∴a4+a8+a12+…+a4n+4=4(n+1)+$\frac{n(n+1)}{2}$•4=2n2+6n+4.
故答案為:2n2+6n+4.
點評 本題考查等差數列的通項及前n項和,考查運算求解能力,注意解題方法的積累,屬于中檔題.


 高中必刷題系列答案
高中必刷題系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 如圖所示,O是坐標原點,兩個正方形OABC、BDEF的頂點中,O、A、C、D、F五個點都在拋物線y2=2px(p>0)上,另外,B、E兩個點都在x軸上,若這兩個正方形的面積之和為10,則( )
如圖所示,O是坐標原點,兩個正方形OABC、BDEF的頂點中,O、A、C、D、F五個點都在拋物線y2=2px(p>0)上,另外,B、E兩個點都在x軸上,若這兩個正方形的面積之和為10,則( )| A. | p=1 | B. | p=2 | C. | p=$\frac{1}{2}$ | D. | p=$\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
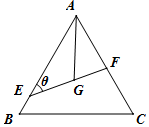 如圖所示,△ABC是邊長為6的等邊三角形,G是它的重心(三條中線的交點),過G的直線分別交線段AB、AC于E、F兩點,∠AEG=θ.
如圖所示,△ABC是邊長為6的等邊三角形,G是它的重心(三條中線的交點),過G的直線分別交線段AB、AC于E、F兩點,∠AEG=θ.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com