Question

16．四面體D-ABC中，AB=BC，在側面DAC中，中線AN⊥中線DM，且DB⊥AN．
（1）求證：MN∥面DAB；
（2）平面ACD⊥平面ABC．

Answer 1

分析 （1）連接MN，由已知可得MN∥AD，再由線面平行的判定可得MN∥平面ABD；
（2）AN⊥DM，AN⊥DB，由線面垂直的判定可得AN⊥平面BDM，得到AN⊥BM，在△ABC中，再由已知可得AC⊥BM．由線面垂直的判定可得BM⊥平面ACD，進一步得到平面ACD⊥平面ABC．

解答 證明：（1）連接MN，∵CN=ND，CM=MA，∴MN∥AD，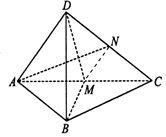
∵MN?平面ABD，AD?平面ABD，∴MN∥平面ABD；
（2）∵AN⊥DM，AN⊥DB，且DB∩DM=D，
∴AN⊥平面BDM，
∵BM?平面BDM，∴AN⊥BM，
又∵△ABC中，AB=BC，且M為AC的中點，∴AC⊥BM．
∵AN，AC時平面ACD內的兩條相交直線，
∴BM⊥平面ACD，
∵BM?平面ABC，∴平面ACD⊥平面ABC．

點評 本題考查直線與平面平行，平面與平面垂直的判定，考查空間想象能力和思維能力，是中檔題．