
分析 (1)f(x)=(log4x-1)(log2x-1)=$(\frac{1}{2}lo{g}_{2}x-1)$(log2x-1),x∈[2,4],令t=log2x∈[1,2],通過換元利用二次函數的單調性即可得出.
(2)x∈[8,16],可得log4x>0,不等式$f(x)≥\frac{m}{{{{log}_4}x}}$恒成立?m≤(log4x-1)(log2x-1)log4x.利用對數函數的單調性即可得出.
解答 解:(1)f(x)=(log4x-1)(log2x-1)=$(\frac{1}{2}lo{g}_{2}x-1)$(log2x-1),
∵x∈[2,4],令t=log2x∈[1,2],
∴f(t)=$(\frac{1}{2}t-1)(t-1)$=$\frac{1}{2}{t}^{2}$-$\frac{3}{2}t$+1=$\frac{1}{2}(t-\frac{3}{2})^{2}$-$\frac{1}{8}$,
∴函數f(t)在$[1,\frac{3}{2}]$上單調遞減;在$[\frac{3}{2},2]$上單調遞增.
∴f(t)min=-$\frac{1}{8}$,f(t)max=f(1)=f(2)=0.
(2)∵x∈[8,16],∴log4x>0,
∴不等式$f(x)≥\frac{m}{{{{log}_4}x}}$恒成立?m≤(log4x-1)(log2x-1)log4x.
log4-1≥log48-1=$\frac{1}{2}$,log2x-1≥log48-1=2,
log4x≥log48=$\frac{3}{2}$.
∴(log4x-1)(log2x-1)log4x≥$\frac{1}{2}×2×\frac{3}{2}$=$\frac{3}{2}$,當且僅當x=8時取等號.
∴$m≤\frac{3}{2}$.
點評 本題考查了對數的運算性質、對數函數的單調性、二次函數的單調性、不等式的性質,考查了推理能力與計算能力,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 四棱錐P-BCDE,底面BCDE為等腰梯形,CB∥DE,PO⊥底面BCDE,F為PB中點,O為BC中點,PO=$\sqrt{3}$,BC=4,DE=CD=BE=2
四棱錐P-BCDE,底面BCDE為等腰梯形,CB∥DE,PO⊥底面BCDE,F為PB中點,O為BC中點,PO=$\sqrt{3}$,BC=4,DE=CD=BE=2查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,3$\sqrt{2}$) | B. | (3$\sqrt{2}$,+∞) | C. | (-∞,3$\sqrt{2}$) | D. | (0,$\sqrt{2}$)∪(3$\sqrt{2}$,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 必要非充分條件 | B. | 充分非必要條件 | ||
| C. | 充要條件 | D. | 非充分非必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
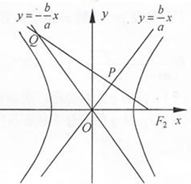 過雙曲線$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\;(a>0,b>0)$的右焦點F2向其一條漸近線作垂線l,垂足為P,l與另一條漸近線交于Q點,若$\overrightarrow{Q{F}_{2}}$=3$\overrightarrow{P{F}_{2}}$,則雙曲線的離心率為( )
過雙曲線$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\;(a>0,b>0)$的右焦點F2向其一條漸近線作垂線l,垂足為P,l與另一條漸近線交于Q點,若$\overrightarrow{Q{F}_{2}}$=3$\overrightarrow{P{F}_{2}}$,則雙曲線的離心率為( )| A. | 2 | B. | $\sqrt{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com