
分析 直接由有理指數冪的運算性質和對數的運算性質化簡計算得答案.
解答 解:(1)${(2\frac{7}{9})^{0.5}}+{0.1^{-2}}+{(2\frac{10}{27})^{-\frac{2}{3}}}-3{π^0}+\frac{37}{48}$
=$(\frac{25}{9})^{\frac{1}{2}}+(\frac{1}{10})^{-2}+(\frac{64}{27})^{-\frac{2}{3}}-3+\frac{37}{48}$
=$\frac{5}{3}+100+\frac{9}{16}-3+\frac{37}{48}$
=100;
(2)$\root{3}{{a}^{\frac{7}{2}}\sqrt{{a}^{-3}}}$÷$\sqrt{\root{3}{{a}^{-8}}\root{3}{a^{16}}}$÷$\root{3}{\sqrt{{a}^{-3}}\sqrt{{a}^{-1}}}$
=$\root{3}{{a}^{\frac{7}{2}}{a}^{-\frac{3}{2}}}$÷$\sqrt{{a}^{-\frac{8}{3}}{a}^{\frac{16}{3}}}$÷$\root{3}{{a}^{-\frac{3}{2}}{a}^{-\frac{1}{2}}}$
=$\root{3}{{a}^{2}}÷\sqrt{{a}^{\frac{8}{3}}}÷\root{3}{{a}^{-2}}$
=${a}^{\frac{2}{3}}$$÷{a}^{\frac{4}{3}}$$÷{a}^{-\frac{2}{3}}$
=${a}^{\frac{2}{3}-\frac{4}{3}+\frac{2}{3}}=1$;
(3)$\frac{lg8+lg125-lg2-lg5}{{lg\sqrt{10}•lg0.1}}$=$\frac{lg\frac{8×125}{2×5}}{\frac{1}{2}lg10•lg\frac{1}{10}}$=$\frac{2}{-\frac{1}{2}}=-4$;
(4)$lg500+lg\frac{8}{5}-\frac{1}{2}lg64+50{(lg2+lg5)^2}$=$lg500×\frac{8}{5}-lg8+50$=lg800-lg8+50=2+lg8-lg8+50=52.
點評 本題考查了有理指數冪的運算性質和對數的運算性質,是基礎題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | y=-$\frac{1}{x}$ | B. | y=-x2+2x+1 | C. | y=$\frac{x}{1-x}$+2 | D. | y=1+x2. |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -12 | B. | 12 | C. | 6 | D. | -6 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
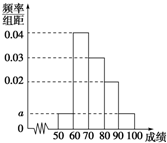 某班100名學生期中考試語文成績的頻率分布直方圖如圖所示,其中成績分組區間是:[50,60),[60,70),[70,80),[80,90),[90,100].
某班100名學生期中考試語文成績的頻率分布直方圖如圖所示,其中成績分組區間是:[50,60),[60,70),[70,80),[80,90),[90,100].| 分數段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x:y | 1:1 | 2:1 | 3:4 | 4:5 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com