
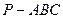 中,
中,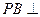 底面
底面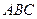 于
于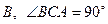 ,
,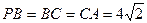 ,點
,點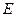 ,點
,點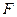 分別是
分別是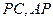 的中點.
的中點.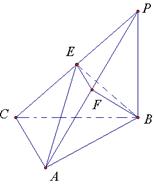
 ⊥側(cè)面
⊥側(cè)面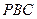 ;
;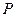 到平面
到平面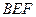 的距離;
的距離;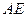 與
與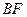 所成的角的余弦.
所成的角的余弦.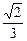
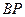 所在直線為
所在直線為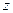 軸,
軸,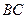 所在直線
所在直線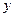 軸,建立空間直角坐標(biāo)系,由條件可設(shè)
軸,建立空間直角坐標(biāo)系,由條件可設(shè)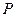 (0,0,4
(0,0,4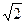 ),
), 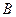 (0,0,0),
(0,0,0), 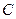 (0,–4
(0,–4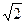 ,0),
,0),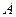 (4
(4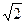 ,–4
,–4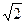 ,0);
,0);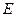 (0,–2
(0,–2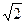 ,2
,2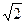 ),
),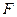 (2
(2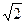 ,–2
,–2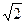 ,2
,2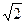 ), --- 2分
), --- 2分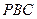 的法向量
的法向量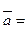 (1,0,0 ), 而
(1,0,0 ), 而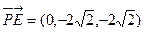 ,
,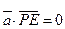 , 所以側(cè)面
, 所以側(cè)面 ⊥側(cè)面
⊥側(cè)面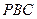 ; --- 2分
; --- 2分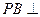 底面
底面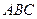 , ∴ 平面
, ∴ 平面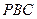 ⊥平面
⊥平面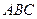 , --- 2分
, --- 2分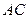 ⊥
⊥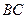 ,∴
,∴ 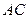 ⊥平面
⊥平面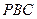 , ∴ 側(cè)面
, ∴ 側(cè)面 ⊥側(cè)面
⊥側(cè)面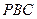 ;) . --- 2分
;) . --- 2分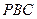 中,
中, 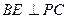 , 又中位線
, 又中位線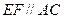 , 而由(1)
, 而由(1)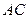 ⊥平面
⊥平面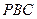 , 則
, 則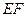 ⊥平面
⊥平面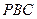 , ∴
, ∴ 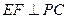 , --- 2分
, --- 2分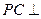 平面
平面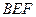 , 那么線段
, 那么線段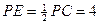 即為點
即為點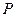 到平面
到平面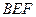 的距離. --- 2分
的距離. --- 2分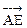 =(–4
=(–4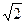 ,2
,2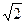 ,2
,2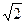 ),
), 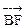 =(2
=(2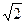 ,–2
,–2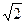 ,2
,2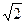 ),
),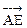 ·
·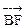 ="–16," 又|
="–16," 又|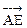 |·|
|·|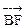 |=24
|=24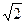 , --- 2分
, --- 2分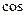 <
<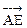 ,
,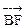 >=–
>=–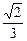 ,
, 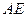 與
與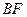 所成的角的余弦值是
所成的角的余弦值是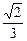 . --- 2分
. --- 2分


| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
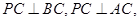 點E,F(xiàn),G分別是所在棱的中點,則下面結(jié)論中正確的是: 。
點E,F(xiàn),G分別是所在棱的中點,則下面結(jié)論中正確的是: 。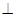 平面ABC
平面ABC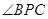 是直線EF與直線PC所成的角
是直線EF與直線PC所成的角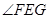 是平面PAB與平面ABC所成二面角的平面角
是平面PAB與平面ABC所成二面角的平面角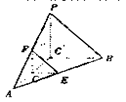
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
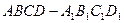 中,底面
中,底面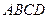 是
是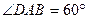 的菱形,
的菱形,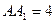 ,
,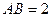 ,點
,點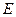 在棱
在棱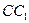 上,點
上,點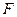 是棱
是棱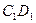 的中點.
的中點.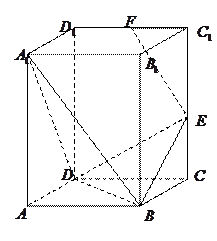
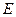 是
是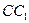 的中點,求證:
的中點,求證: ;
;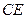 的長度,使得
的長度,使得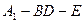 為直二面角.
為直二面角.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
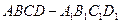 中,棱長為
中,棱長為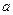
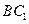 與
與 所成的角;
所成的角;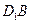 與平面
與平面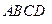 所成角的正切值;
所成角的正切值;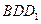
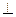 平面
平面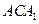 .
.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
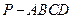 的底面為直角梯形,
的底面為直角梯形, ,
,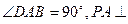 底面
底面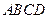 ,且
,且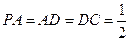 ,
, ,
,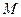 是
是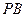 的中點。
的中點。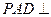 面
面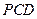 ;
;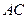 與
與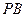 所成角的余弦值;
所成角的余弦值;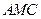 與面
與面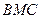 所成二面角的余弦值.
所成二面角的余弦值.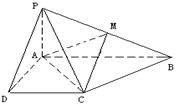
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
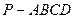 中,
中,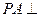 底面
底面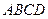 ,
,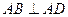 ,
,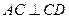 ,
,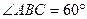 ,
,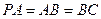 ,
,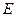 是
是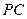 的中點.
的中點.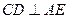 ;
;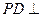 面
面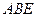 ;
;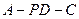 的平面角的正弦值.
的平面角的正弦值.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
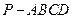 中,底面
中,底面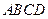 是矩形,
是矩形,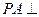 平面
平面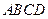 ,
,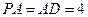 ,
,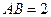 . 以
. 以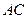 的中點
的中點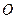 為球心、
為球心、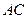 為直徑的球面交
為直徑的球面交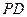 于點
于點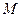 ,交
,交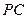 于點
于點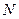 .
.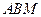 ⊥平面
⊥平面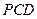 ;
;
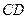 與平面
與平面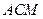 所成的角的正弦值.
所成的角的正弦值.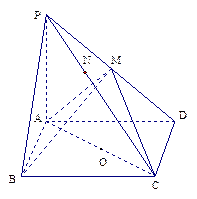
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
 AB-C2為60o,
AB-C2為60o, 則點C
則點C 1與C2之間的距離可能是___________.(寫出二個可能值即可)
1與C2之間的距離可能是___________.(寫出二個可能值即可)查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com