
【題目】已知函數f(x)=log ![]() (x2﹣ax+b). (Ⅰ)若函數f(x)的定義域為(﹣∞,2)∪(3,+∞),求實數a,b的值;
(x2﹣ax+b). (Ⅰ)若函數f(x)的定義域為(﹣∞,2)∪(3,+∞),求實數a,b的值;
(Ⅱ)若f(﹣2)=﹣3且f(x)在(﹣∞,﹣1]上為增函數,求實數b的取值范圍.
【答案】解:(Ⅰ)由題意,不等式x2﹣ax+b>0 的解集是 (﹣∞,2)∪(3,+∞), 所以2,3是方程x2﹣ax+b=0 的兩實根,
∴2+3=a且2×3=b,
即a=5,b=6
(Ⅱ)設g(x)=x2﹣ax+b,
由f(﹣2)=﹣3得g(﹣2)=4+2a+b=8,
即a= ![]() (4﹣b)
(4﹣b)
又 f(x)在(﹣∞,﹣1]上為增函數,
所以g(x)=x2﹣ax+b在(﹣∞,﹣1]上是減函數且恒為正數,
∴ 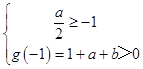 ,
,
也即 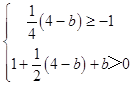 ,
,
解得:b∈(﹣6,8]
【解析】(Ⅰ)由題意,不等式x2﹣ax+b>0 的解集是 (﹣∞,2)∪(3,+∞),所以2,3是方程x2﹣ax+b=0 的兩實根,由韋達定理,可得實數a,b的值;(Ⅱ) 設g(x)=x2﹣ax+b,若f(﹣2)=﹣3且f(x)在(﹣∞,﹣1]上為增函數,則g(﹣2)=8,g(x)=x2﹣ax+b在(﹣∞,﹣1]上是減函數且恒為正數,進而可得實數b的取值范圍.
【考點精析】本題主要考查了二次函數的性質的相關知識點,需要掌握當![]() 時,拋物線開口向上,函數在
時,拋物線開口向上,函數在![]() 上遞減,在
上遞減,在![]() 上遞增;當
上遞增;當![]() 時,拋物線開口向下,函數在
時,拋物線開口向下,函數在![]() 上遞增,在
上遞增,在![]() 上遞減才能正確解答此題.
上遞減才能正確解答此題.


 星級口算天天練系列答案
星級口算天天練系列答案 芒果教輔達標測試卷系列答案
芒果教輔達標測試卷系列答案科目:高中數學 來源: 題型:
【題目】集合A={x|3≤x<9},B={x|1<x<7},C={x|x>m}.
(1)求A∪B;
(2)求(RA)∩B;
(3)若BC,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩種不同規格的產品,其質量按測試指標分數進行劃分,其中分數不小于82分的為合格品,否則為次品.現隨機抽取兩種產品各100件進行檢測,其結果如下:
測試指標分數 |
|
|
|
|
|
甲產品 | 8 | 12 | 40 | 32 | 8 |
乙產品 | 7 | 18 | 40 | 29 | 6 |
(1)根據以上數據,完成下面的![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的有把握認為兩種產品的質量有明顯差異?
的有把握認為兩種產品的質量有明顯差異?
甲產品 | 乙產品 | 合計 | |
合格品 | |||
次品 | |||
合計 |
(2)已知生產1件甲產品,若為合格品,則可盈利40元,若為次品,則虧損5元;生產1件乙產品,若為合格品,則可盈利50元,若為次品,則虧損10元.記![]() 為生產1件甲產品和1件乙產品所得的總利潤,求隨機變量
為生產1件甲產品和1件乙產品所得的總利潤,求隨機變量![]() 的分布列和數學期望(將產品的合格率作為抽檢一件這種產品為合格品的概率).
的分布列和數學期望(將產品的合格率作為抽檢一件這種產品為合格品的概率).
附:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.702 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率
的離心率![]() ,兩焦點分別為
,兩焦點分別為![]() ,右頂點為
,右頂點為![]() ,
, ![]() .
.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)設過定點![]() 的直線
的直線![]() 與雙曲線
與雙曲線![]() 的左支有兩個交點,與橢圓
的左支有兩個交點,與橢圓![]() 交于
交于![]() 兩點,與圓
兩點,與圓![]() 交于
交于![]() 兩點,若
兩點,若![]() 的面積為
的面積為![]() ,
, ![]() ,求正數
,求正數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種商品價格與該商品日需求量之間的幾組對照數據如下表:

(1)求關于的線性回歸方程;
(2)利用(1)中的回歸方程,當價格![]() 元
元![]() 時,日需求量
時,日需求量![]() 的預測值為多少?
的預測值為多少?
參考公式:線性歸回方程: ![]() ,其中
,其中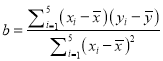 ,
, ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com