【題目】已知拋物線
：
的焦點為
，拋物線上存在一點
到焦點的距離等于3.
（1）求拋物線的方程；
（2）過點的直線
交拋物線于
，
兩點，以線段
為直徑的圓交
軸于
，
兩點，設線段的中點為
，求
的最小值.
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】已知
，
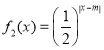，其中
．
（1）若
，令函數
，解不等式
；
（2）若
，
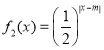，求的值域；
（3）設函數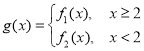
，若對于任意大于等于2的實數
，總存在唯一的小于2的實數
，使得
成立，試確定實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】過去大多數人采用儲蓄的方式將錢儲蓄起來，以保證自己生活的穩定，考慮到通貨膨脹的壓力，如果我們把所有的錢都用來儲蓄，這并不是一種很好的方式，隨著金融業的發展，普通人能夠使用的投資理財工具也多了起來，為了研究某種理財工具的使用情況，現對
年齡段的人員進行了調查研究，將各年齡段人數分成5組，
，
，
，
，
，并整理得到頻率分布直方圖：
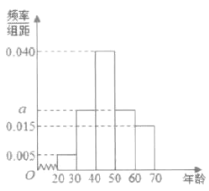
（Ⅰ）求圖中的
值；
（Ⅱ）求被調查人員的年齡的中位數和平均數；
（Ⅲ）采用分層抽樣的方法，從第二組、第三組、第四組中共抽取8人，在抽取的8人中隨機抽取2人，則這2人都來自于第三組的概率是多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，在長方體
中，已知
，
．
（1）求：凸多面體
的體積；
（2）若
為線段
的中點，求點到平面
的距離；
（3）若點
、
分別在棱
、
上滑動，且線段
的長恒等于
，線段的中點為
①試證：點必落在過線段的中點且平行于底面
的平面上；
②試求點的軌跡．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】定義：若存在常數
，使得對定義域D內的任意兩個不同的實數
，均有：
成立，則稱
在D上滿足利普希茨(Lipschitz)條件．
（1）試舉出一個滿足利普希茨(Lipschitz)條件的函數及常數的值，并加以驗證；
（2）若函數
在
上滿足利普希茨(Lipschitz)條件，求常數的最小值；
（3)現有函數
，請找出所有的一次函數
，使得下列條件同時成立：
①函數滿足利普希茨(Lipschitz)條件；
②方程
的根
也是方程
的根，且
；
③方程
在區間
上有且僅有一解．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知定義在
上的函數
滿足：①對任意
，存在正常數
，都有
成立；②的值域為
(
)，則函數是（ ）
A.周期為2的周期函數B.周期為4的周期函數
C.奇函數D.偶函數
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某餐廳通過查閱了最近5次食品交易會參會人數
(萬人)與餐廳所用原材料數量
(袋)，得到如下統計表：
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
參會人數 | 13 | 9 | 8 | 10 | 12 |
原材料 | 32 | 23 | 18 | 24 | 28 |
（1）根據所給5組數據，求出
關于
的線性回歸方程
.
（2）已知購買原材料的費用
(元)與數量
(袋)的關系為
，
投入使用的每袋原材料相應的銷售收入為700元，多余的原材料只能無償返還，據悉本次交易大會大約有15萬人參加，根據(1)中求出的線性回歸方程，預測餐廳應購買多少袋原材料，才能獲得最大利潤，最大利潤是多少？(注：利潤
銷售收入
原材料費用).
參考公式： 
， 
.
參考數據： 
， 
， 
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某環線地鐵按內、外環線同時運行，內、外環線的長均為30千米（忽略內、外環線長度差異）．
（1）當9列列車同時在內環線上運行時，要使內環線乘客最長候車時間為10分鐘，求內環線列車的最小平均速度；
（2）新調整的方案要求內環線列車平均速度為25千米/小時，外環線列車平均速度為30千米/小時．現內、外環線共有18列列車全部投入運行，要使內外環線乘客的最長候車時間之差不超過1分鐘，向內、外環線應各投入幾列列車運行？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一個口袋中裝有9個大小形狀完全相同的球，球的編號分別為1，2，…，9，隨機摸出兩個球，則兩個球的編號之和大于9的概率是______（結果用分數表示）.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
