【題目】一個口袋中裝有9個大小形狀完全相同的球，球的編號分別為1，2，…，9，隨機摸出兩個球，則兩個球的編號之和大于9的概率是______（結果用分數表示）.
【答案】
【解析】
由題意分別列舉兩個球編號之和大于9的號碼，再用古典概型公式求概率．
解：當抽出的其中一個球為1號時，另一個球的號碼為9，
當抽出的其中一個球為2號時，另一個球的號碼為9，8，
當抽出的其中一個球為3號時，另一個球的號碼為9，8，7，
當抽出的其中一個球為4號時，另一個球的號碼為9，8，7，6，
當抽出的其中一個球為5號時，另一個球的號碼為9，8，7，6，
當抽出的其中一個球為6號時，另一個球的號碼為9，8，7，
當抽出的其中一個球為7號時，另一個球的號碼為9，8，
當抽出的其中一個球為8號時，另一個球的號碼為9，
所以兩個球編號之和大于9的情況有1＋2＋3＋4＋4＋3＋2＋1＝20種，
總的抽取情況有
種，所以兩個球編號之和大于9的概率是
，
故答案為：．
科目：高中數學 來源： 題型：
【題目】已知拋物線
：
的焦點為
，拋物線上存在一點
到焦點的距離等于3.
（1）求拋物線的方程；
（2）過點的直線
交拋物線于
，
兩點，以線段
為直徑的圓交
軸于
，
兩點，設線段的中點為
，求
的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的左右焦點分別為
，離心率為
；圓
過橢圓
的三個頂點.過點
且斜率不為0的直線
與橢圓交于
兩點.
（Ⅰ）求橢圓的標準方程；
（Ⅱ）證明：在
軸上存在定點
，使得
為定值；并求出該定點的坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】《九章算術》中，將底面為長方形且有一條側棱與地面垂直的四棱錐稱之為陽馬，將四個面都為直角三角形的四面體稱之為鱉臑，首屆中國國際進口博覽會的某展館棚頂一角的鋼結構可以抽象為空間圖形陽馬，如圖所示，在陽馬
中，
底面
.
（1）已知
，斜梁
與底面所成角為
，求立柱
的長；（精確到
）
（2）求證：四面體
為鱉臑.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
（其中
，
，
，
是實數常數，
）.
（1）若
，函數
的圖象關于點
成中心對稱，求，的值；
（2）若函數滿足條件（1），且對任意
，總有
，求的取值范圍；
（3）若
，函數是奇函數，
，
，且對任意
時，不等式
恒成立，求負實數
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】十七世紀，法國數學家費馬提出猜想；“當整數
時，關于
、
、
的方程
沒有正整數解”，經歷三百多年，1995年英國數學家安德魯
懷爾斯給出了證明，使它終成費馬大定理，則下面命題正確的是（ ）
①對任意正整數
，關于、、的方程都沒有正整數解；
②當整數時，關于、、的方程至少存在一組正整數解；
③當正整數
時，關于、、的方程至少存在一組正整數解；
④若關于、、的方程至少存在一組正整數解，則正整數；
A.①②/span>B.①③C.②④D.③④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】無窮數列
、
、
滿足：
，
，
，
，記
（
表示3個實數
、
、
中的最大數）.
（1）若
，
，
，求數列
的前
項和
；
（2）若
，
，
，當
時，求滿足條件
的
的取值范圍；
（3）證明：對于任意正整數
、
、
，必存在正整數
，使得
，
，
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
：
的左右焦點為
，
，
是橢圓上半部分的動點，連接和長軸的左右兩個端點所得兩直線交
正半軸于
，
兩點（點在的上方或重合）.
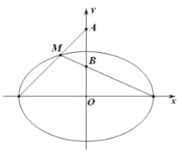
（1）當
面積
最大時，求橢圓的方程；
（2）當
時，若是線段
的中點，求直線
的方程；
（3）當
時，在
軸上是否存在點
使得
為定值，若存在，求點的坐標，若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某種商品原來毎件售價為25元,年銷售8萬件.
(1)據市場調查，若價格毎提高1元，銷售量將相應瑊少2000件,要使銷售的總收入不低于原收入，該商品每件定價最多為多少？
(2)為了擴大商品的影響力,提高年銷售量，公司決定明年對該商品進行全面技術革新和營銷策略改革,并提高價格到
元,公司擬投入
萬元作為技改費用,投入50萬元作為固定宣傳費用，試問:該商品明年的銷售量
至少達到多少萬件時,才可能使明年的銷售收入不低于原收入與總投入之和?并求出此時每件商品的定價.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com