
【題目】
已知函數![]() =(sin x+cos x)2+cos 2x.
=(sin x+cos x)2+cos 2x.
(1)求函數![]() 的最小正周期;
的最小正周期;
(2)求函數![]() 在區間
在區間![]() 上的最大值和最小值.
上的最大值和最小值.
【答案】(1)![]() (2)f(x)在
(2)f(x)在![]() 上的最大值為
上的最大值為![]() +1,最小值為0.
+1,最小值為0.
【解析】試題分析: ![]() 根據二倍角公式和兩角和的正弦公式對
根據二倍角公式和兩角和的正弦公式對![]() 化簡,得到
化簡,得到![]() 的形式,利用最小正周期計算公式即可求解;
的形式,利用最小正周期計算公式即可求解;
![]() 根據定義域求出
根據定義域求出![]() 的取值范圍,進而得到
的取值范圍,進而得到![]() 的取值范圍,從而得到函數
的取值范圍,從而得到函數![]() 的最值。
的最值。
解析:(1)因為f(x)=sin2x+cos2x+2sin xcos x+cos 2x=1+sin 2x+cos 2x=![]() sin
sin![]() +1,
+1,
所以函數f(x)的最小正周期T=![]() =π.
=π.
(2)由(1)知,f(x)=![]() sin
sin![]() +1.
+1.
當x∈![]() 時,2x+
時,2x+![]() ∈
∈![]() ,
,
由正弦函數y=sin x在![]() 上的圖象知,
上的圖象知,
當2x+![]() =
=![]() ,即x=
,即x=![]() 時,f(x)取最大值
時,f(x)取最大值![]() +1;
+1;
當2x+![]() =
=![]() ,即x=
,即x=![]() 時,f(x)取最小值0.
時,f(x)取最小值0.
綜上,f(x)在![]() 上的最大值為
上的最大值為![]() +1,最小值為0.
+1,最小值為0.


科目:高中數學 來源: 題型:
【題目】已知橢圓E: ![]() 的焦點在
的焦點在 ![]() 軸上,A是E的左頂點,斜率為k(k>0)的直線交E于A,M兩點,點N在E上,MA⊥NA.
軸上,A是E的左頂點,斜率為k(k>0)的直線交E于A,M兩點,點N在E上,MA⊥NA.
(1)當t=4, ![]() 時,求△AMN的面積;
時,求△AMN的面積;
(2)當 ![]() 時,求k的取值范圍.
時,求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現需要設計一個倉庫,它由上下兩部分組成,上部的形狀是正四棱錐P﹣A1B1C1D1 , 下部的形狀是正四棱柱ABCD﹣A1B1C1D1(如圖所示),并要求正四棱柱的高O1O是正四棱錐的高PO1的4倍.
(1)若AB=6m,PO1=2m,則倉庫的容積是多少?
(2)若正四棱柱的側棱長為6m,則當PO1為多少時,倉庫的容積最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】成等差數列的三個正數的和等于15,并且這三個數分別加上2、5、13后成為等比數列{bn}中的b3、b4、b5.
(Ⅰ)求數列{bn}的通項公式;
(Ⅱ)數列{bn}的前n項和為Sn,求證:數列{Sn+![]() }是等比數列.
}是等比數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高校調查了200名學生每周的自習時間(單位:小時),制成了如圖所示的頻率分布直方圖,其中自習時間的范圍是[17.5,30],樣本數據分組為[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根據直方圖,這200名學生中每周的自習時間不少于22.5小時的人數是( )
A.56
B.60
C.120
D.140
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】觀察下列等式:
(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2=
)﹣2= ![]() ×1×2;
×1×2;
(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+sin(
)﹣2+sin( ![]() )﹣2=
)﹣2= ![]() ×2×3;
×2×3;
(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+…+sin(
)﹣2+…+sin( ![]() )﹣2=
)﹣2= ![]() ×3×4;
×3×4;
(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+…+sin(
)﹣2+…+sin( ![]() )﹣2=
)﹣2= ![]() ×4×5;
×4×5;
…
照此規律,
(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+…+(sin
)﹣2+…+(sin ![]() )﹣2= .
)﹣2= .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和Sn=3n2+8n,{bn}是等差數列,且an=bn+bn+1 .
(1)求數列{bn}的通項公式;
(2)令cn= ![]() ,求數列{cn}的前n項和Tn .
,求數列{cn}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在平面斜坐標系xOy中,∠xOy=60°,平面上任意一點P關于斜坐標系的斜坐標是這樣定義的:若![]() =xe1+ye2(其中e1,e2分別為x軸、y軸同方向的單位向量),則點P的斜坐標為(x,y).
=xe1+ye2(其中e1,e2分別為x軸、y軸同方向的單位向量),則點P的斜坐標為(x,y).
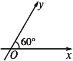
(1)若點P在斜坐標系xOy中的斜坐標為(2,-2),求點P到原點O的距離.
(2)求以原點O為圓心,1為半徑的圓在斜坐標系xOy中的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com