Question

4．已知函數f（x）=x²+2x|x-a|，其中a∈R．
（1）當a=-1時，在所給坐標系中作出f（x）的圖象；
（2）對任意x∈[1，2]，函數g（x）=-x+14的圖象恒在函數f（x）圖象的上方，求實數a的取值范圍．

Answer 1

分析 （1）當a=-1時，作出函數f（x）=x²+2x|x+1|=$\left\{\begin{array}{l}{{-x}^{2}-2x，x＜-1}\\{{3x}^{2}+2x，x≥-1}\end{array}\right.$ 的圖象．
（Ⅱ）由題意，對任意x∈[1，2]，只需[f（x）+x]_max＜14．分類討論求得[f（x）+x]_max ，可得實數a的取值范圍．

解答 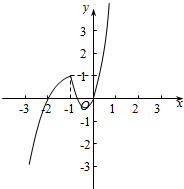解：（1）當a=-1時，作出函數f（x）=x²+2x|x-a|=x²+2x|x+1|=$\left\{\begin{array}{l}{{-x}^{2}-2x，x＜-1}\\{{3x}^{2}+2x，x≥-1}\end{array}\right.$ 的圖象，
如圖所示：
（2）由題意，對任意x∈[1，2]，f（x）＜g（x），
即f（x）+x＜14恒成立，
只需[f（x）+x）]_max＜14．
另一方面，f（x）=$\left\{\begin{array}{l}{{-x}^{2}+2ax，x＜a}\\{{3x}^{2}-2ax，x≥a}\end{array}\right.$．
當a≥0時，f（x）在（-∞，a）和（a，+∞）上均遞增，∵f（a）=a²，則f（x）在R上遞增，
當a＜0時，f（x）在（-∞，a）和（$\frac{a}{3}$，+∞）上遞增，在（a，$\frac{a}{3}$）上遞減，
故f（x）在x∈[1，2]上恒單調遞增，從而y=f（x）+x在x∈[1，2]上也恒單調遞增，
則[f（x）+x]_max=f（2）+2=4+4|2-a|+2＜14，即|2-a|＜2，解得0＜a＜4，
故實數a的取值范圍是（0，4）．

點評 本題主要考查函數的圖象，函數與方程的綜合應用，體現了轉化、分類討論的數學思想，屬于中檔題．