
分析 根據$|\overrightarrow{a}|=4,|\overrightarrow{b}|=2$,進行數量積的運算,便可由$(\overrightarrow{a}+2\overrightarrow{b})•(\overrightarrow{a}+\overrightarrow{b})=12$求出$cos<\overrightarrow{a},\overrightarrow{b}>$的值,進而求出向量$\overrightarrow{a},\overrightarrow{b}$的夾角.
解答 解:根據條件:
$(\overrightarrow{a}+2\overrightarrow{b})•(\overrightarrow{a}+\overrightarrow{b})={\overrightarrow{a}}^{2}+2{\overrightarrow{b}}^{2}+3\overrightarrow{a}•\overrightarrow{b}$=$16+8+24cos<\overrightarrow{a},\overrightarrow{b}>=12$;
∴$cos<\overrightarrow{a},\overrightarrow{b}>=-\frac{1}{2}$;
又$0≤<\overrightarrow{a},\overrightarrow{b}>≤π$;
∴$\overrightarrow{a}$與$\overrightarrow{b}$的夾角為$\frac{2π}{3}$.
故答案為:$\frac{2π}{3}$.
點評 本題考查數量積的運算及計算公式,向量夾角的范圍,已知三角函數值求角.


科目:高中數學 來源: 題型:解答題
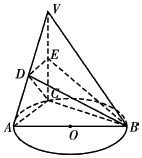 如圖AB是圓O的直徑,點C是弧AB上一點,VC垂直圓O所在平面,D,E分別為VA,VC的中點.
如圖AB是圓O的直徑,點C是弧AB上一點,VC垂直圓O所在平面,D,E分別為VA,VC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $a+\frac{1}{b}>b+\frac{1}{a}$ | B. | $\frac{b}{a}>\frac{b+1}{a+1}$ | C. | $a-\frac{1}{b}>b-\frac{1}{a}$ | D. | $\frac{2a+b}{a+2b}>\frac{a}{b}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{1}{12}$ | D. | -$\frac{1}{12}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com