
【題目】已知函數![]()
![]() .
.
(Ⅰ)若![]() 在區間
在區間![]() 上有極值,求實數
上有極值,求實數![]() 的取值范圍;
的取值范圍;
(Ⅱ)若![]() 有唯一的零點
有唯一的零點![]() ,試求
,試求![]() 的值.(注:
的值.(注:![]() 為取整函數,表示不超過
為取整函數,表示不超過![]() 的最大整數,如
的最大整數,如![]() ;以下數據供參考:
;以下數據供參考:![]() )
)
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)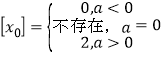 .
.
【解析】
試題分析:(1)求出f(x)的導數,令h(x)=2x3﹣ax﹣2,x∈(0,+∞),求出導數,討論a的符號,判斷單調性,即可得到所求a的范圍;(2)由(1)可知:f(1)=3知x∈(0,1)時,f(x)>0,則x0>1,討論f(x)在x>1的單調性,再由零點的定義和極值點的定義,可得x0的方程,構造函數![]() ,判斷單調性,由零點存在性定理知 t(2)<0,t(3)>0,即可得到所求值.
,判斷單調性,由零點存在性定理知 t(2)<0,t(3)>0,即可得到所求值.
試題解析:
(Ⅰ)函數![]()
![]() 的定義域為
的定義域為![]() ,
,
![]()
令![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() 恒成立,
恒成立,![]() 在
在![]() 上為增函數,
上為增函數,
又![]() 函數
函數![]() 在
在![]() 內有一個零點
內有一個零點![]() ,
,
且當![]() 時,
時,![]() 時,
時,![]() ,
,
所以![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
所以![]() 在區間
在區間![]() 內有極小值.
內有極小值.
當![]() 時,
時,![]() ,即
,即![]() 時,
時,![]() 恒成立,
恒成立,
![]() 函數
函數![]() 在
在![]() 單調遞減,此時函數
單調遞減,此時函數![]() 無極值,
無極值,
綜上可得:![]() 在區間
在區間![]() 內有極值時實數
內有極值時實數![]() 的取值范圍是
的取值范圍是![]() ,
,
(Ⅱ)①當![]() 時,
時,![]() 得
得![]() ,不滿足定義域,
,不滿足定義域,![]() 不存在.
不存在.
②當![]() 時,由(Ⅰ)知:若
時,由(Ⅰ)知:若![]() 有唯一的零點
有唯一的零點![]() 為極小值點,
為極小值點,
所以![]() ,
,
③當![]() 時,函數
時,函數![]() 的定義域為
的定義域為![]() ,
,
由(Ⅰ)可知:![]() 知
知![]() 時,
時,![]()
又![]() 在區間
在區間![]() 上只有一個極小值點記為
上只有一個極小值點記為![]() ,
,
且![]() 時,
時,![]() 函數
函數![]() 單調遞減,
單調遞減,
![]() 時,
時,![]() ,函數
,函數![]() 單調遞增,
單調遞增,
由題意可知:![]() 即為
即為![]() ,
,
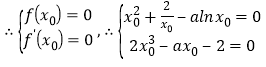 消去可得:
消去可得:![]() ,
,
即![]() ,
,
令![]() ,則
,則![]() 在區間
在區間![]() 上單調遞增,
上單調遞增,
又![]() ,
,
![]() ,
,
由零點存在性定理知![]()
![]()
綜上可得: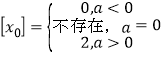


 尖子生新課堂課時作業系列答案
尖子生新課堂課時作業系列答案科目:高中數學 來源: 題型:
【題目】為了引導居民合理用電,國家決定實行合理的階梯電價,居民用電原則上以住宅為單位(一套住宅為一戶).
階梯級別 | 第一階梯 | 第二階梯 | 第三階梯 |
月用電范圍(度) | (0,210] | (210,400] |
|
某市隨機抽取10戶同一個月的用電情況,得到統計表如下:
居民用電戶編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
用電量(度) | 53 | 86 | 90 | 124 | 132 | 200 | 215 | 225 | 300 | 410 |
若規定第一階梯電價每度0.5元,第二階梯超出第一階梯的部分每度0.6元,第三階梯超出第二階梯的部分每度0.8元,試計算A居民用電戶用電410度時應電費多少元?
現要在這10戶家庭中任意選取3戶,求取到第二階梯電量的戶數的分布列與期望;
以表中抽到的10戶作為樣本估計全市的居民用電,現從全市中依次抽取10戶,若抽到![]() 戶用電量為第一階梯的可能性最大,求
戶用電量為第一階梯的可能性最大,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙、丙三人組成一個小組參加電視臺舉辦的聽曲猜歌名活動,在每一輪活動中,依次播放三首樂曲,然后甲猜第一首,乙猜第二首,丙猜第三首,若有一人猜錯,則活動立即結束;若三人均猜對,則該小組進入下一輪,該小組最多參加三輪活動.已知每一輪甲猜對歌名的概率是![]() ,乙猜對歌名的概率是
,乙猜對歌名的概率是![]() ,丙猜對歌名的概率是
,丙猜對歌名的概率是![]() ,甲、乙、丙猜對與否互不影響.
,甲、乙、丙猜對與否互不影響.
(I)求該小組未能進入第二輪的概率;
(Ⅱ)記乙猜歌曲的次數為隨機變量![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)已知矩形的面積為100,則這個矩形的長、寬各為多少時,矩形的周長最短?最短周長是多少?
(2)已知矩形的周長為36,則這個矩形的長、寬各為多少時,它的面積最大?最大面積是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設雙曲線![]() 的左,右焦點分別為F1,F2,過F1的直線l交雙曲線左支于A,B兩點,則|BF2|+|AF2|的最小值為( )
的左,右焦點分別為F1,F2,過F1的直線l交雙曲線左支于A,B兩點,則|BF2|+|AF2|的最小值為( )
A. ![]() B. 11
B. 11
C. 12 D. 16
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在多面體![]() 中,四邊形
中,四邊形![]() 為矩形,
為矩形,![]() ,
,![]() 均為等邊三角形,
均為等邊三角形,![]() ,
,![]() .
.
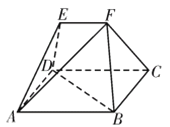
(1)過![]() 作截面與線段
作截面與線段![]() 交于點
交于點![]() ,使得
,使得![]() 平面
平面![]() ,試確定點
,試確定點![]() 的位置,并予以證明;
的位置,并予以證明;
(2)在(1)的條件下,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大型高端制造公司為響應《中國制造2025》中提出的堅持“創新驅動、質量為先、綠色發展、結構優化、人才為本”的基本方針,準備加大產品研發投資,下表是該公司2017年5~12月份研發費用(百萬元)和產品銷量(萬臺)的具體數據:

(1)根據數據可知![]() 與
與![]() 之間存在線性相關關系
之間存在線性相關關系
(i)求出![]() 關于
關于![]() 的線性回歸方程(系數精確到
的線性回歸方程(系數精確到![]() );
);
(ii)若2018年6月份研發投人為25百萬元,根據所求的線性回歸方程估計當月產品的銷量;
(2)公司在2017年年終總結時準備從該年8~12月份這5個月中抽取3個月的數據進行重點分析,求沒有抽到9月份數據的概率.
參考數據: ![]() ,
,![]() .
.
參考公式:對于一組數據![]() ,
,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: 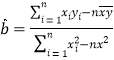 ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com