
| A. | -1 | B. | $-\frac{1}{e}$ | C. | 0 | D. | e |
分析 由設t=f(x)-lnx,則f(x)=lnx+t,又由f(t)=e+1,求出f(x)=lnx+e,再求出jh(x),根據導數和函數的最值的關系即可求出.
解答 解:根據題意,對任意的x∈(0,+∞),都有f[f(x)-lnx]=e+1,
又由f(x)是定義在(0,+∞)上的單調函數,
∴f(x)-lnx為定值,
設t=f(x)-lnx,
∴f(x)=lnx+t,
又由f(t)=e+1,
即lnt+t=e+1,
解得:t=e,
∴f(x)=lnx+e,
∴h(x)=xf(x)-ex=xlnx,
∴h′(x)=1+lnx,
令h′(x)=0,解得x=$\frac{1}{e}$,
當h′(x)>0時,即x>$\frac{1}{e}$,函數h(x)單調遞增,
h′(x)>0時,即0<x<$\frac{1}{e}$,函數h(x)單調遞減,
∴h(x)min=h($\frac{1}{e}$)=-$\frac{1}{e}$,
故選:B.
點評 本題考查了導數的運算和函數的最值,關鍵是求出f(x),屬于中檔題


科目:高中數學 來源: 題型:解答題
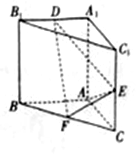 三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=AB=AC=1,E、F分別是CC1、BC的中點,AE⊥A1B1
三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=AB=AC=1,E、F分別是CC1、BC的中點,AE⊥A1B1查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $(-1,-\frac{7}{8})$ | B. | (0,+∞) | C. | (-∞,0) | D. | $(1,\frac{6}{5})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
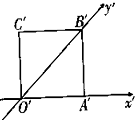 如圖,正方形O′A′B′C′的邊長為2cm,它是水平放置的一個平面圖形的直觀圖,則原平面圖形的周長是( )cm.
如圖,正方形O′A′B′C′的邊長為2cm,它是水平放置的一個平面圖形的直觀圖,則原平面圖形的周長是( )cm.| A. | 12 | B. | 16 | C. | $4(1+\sqrt{3})$ | D. | $4(1+\sqrt{2})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com