Question

1．已知函數f（x）=5x+sinx（x∈R），且f（x²-4x）+f（y²+3）≤0，則當y＞0時，$\frac{y}{x}$+$\frac{x}{y}$的取值范圍是（　　）

• A． $（{0，\frac{{4\sqrt{3}}}{3}}]$
• B． $[{2，\frac{{4\sqrt{3}}}{3}}]$
• C． $[{\frac{{4\sqrt{3}}}{3}，+∞}）$
• D． [2，+∞）

Answer 1

分析 由題意：可知：f（-x）=-f（x）是奇函數，則f（x²-4x）≤f（-y²-3），f′（x）=5-cosx＞0，可知函數單調遞增，可得x²-4x≤-y²-3，求出x與y關系式，k=$\frac{y}{x}$看成斜率的問題，這樣$\frac{y}{x}$+$\frac{x}{y}$=$k+\frac{1}{k}$看成是勾勾函數．即可求解范圍．

解答 解：∵f（x）=5x+sinx（x∈R），
∴f（-x）=-5x-sinx=-（5x+sinx）=-f（x），
即f（x）=5x+sinx（x∈R）是奇函數，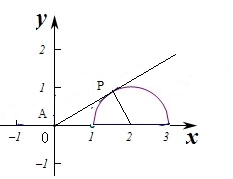
∵f（x²-4x）+f（y²+3）≤0，
∴f（x²-4x）≤f（-y²-3），
由f'（x）=5-cosx＞0，
∴函數單調遞增．
∴x²-4x≤-y²-3，
即y²+x²-4x+4≤1．
當y＞0時，
∴不等式對應的平面區域為圓心為（2，0），半徑為1的圓的上半部分．$\frac{y}{x}$幾何意義是動點P（x，y）到定點A（0，0）的斜率k的取值范圍．
設k=$\frac{y}{x}$（k＞0），則y=kx，即kx-y=0．
當直線和圓相切時，圓心到直線的距離d=$\frac{|2k|}{\sqrt{1+{k}^{2}}}=1$
即3k²-1=0，解得k=$\frac{\sqrt{3}}{3}$．此時直線斜率最大．
令函數t=$\frac{y}{x}$+$\frac{x}{y}$=$k+\frac{1}{k}$，（k＜0≤$\frac{\sqrt{3}}{3}$）
利用勾股函數的性質可知：k∈（0，$\frac{\sqrt{3}}{3}$]是單調減函數．
當k=$\frac{\sqrt{3}}{3}$時，t取得最小值為$\frac{4\sqrt{3}}{3}$．
所以t的取值范圍是[$\frac{4\sqrt{3}}{3}$，+∞）
故選C．

點評 本題主要考查直線和圓的位置關系的應用，函數奇偶性和單調性的判斷以及直線斜率的取值范圍，綜合性較強，運算量較大，利用數形結合是解決本題的基本思想．屬于中檔題．