
分析 (1)由已知及正弦定理可求b2=ac,又$a=\sqrt{2}b$,聯立可得$c=\frac{{\sqrt{2}}}{2}b$,利用余弦定理即可得解cosB的值.
(2)由(1)知b2=ac,利用已知及余弦定理,整理可得c=a=$\sqrt{2}$,進而利用三角形面積公式即可計算得解.
解答 (本題滿分為12分)
解:(1)sin2B=sinAsinC⇒b2=ac①,
又$a=\sqrt{2}b$②,
由①②知$c=\frac{{\sqrt{2}}}{2}b$,…(3分)
所以$cosB=\frac{{{a^2}+{c^2}-{b^2}}}{2ac}=\frac{{2{b^2}+\frac{1}{2}{b^2}-{b^2}}}{{2{b^2}}}=\frac{3}{4}$.…(6分)
(2)由(1)知:b2=ac③,
B=60°,由余弦定理可得:b2=a2+c2-2ac×$\frac{1}{2}$=a2+c2-ac,④,
利用③④可得:a2+c2-ac=ac,即(a-c)2=0,可得:c=a=$\sqrt{2}$,…10分
所以,S△ABC=$\frac{1}{2}$acsinB=$\frac{1}{2}×\sqrt{2}×\sqrt{2}×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$…12分
點評 本題主要考查了正弦定理,余弦定理,三角形面積公式在解三角形中的綜合應用,考查了轉化思想,屬于基礎題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:選擇題
| A. | [1,4] | B. | (-∞,4] | C. | [3,+∞) | D. | (-∞,1]∪[4,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
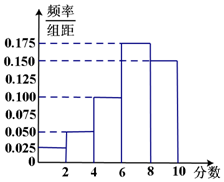 某汽車公司為了考查某4S店的服務態度,對到店維修保養的客戶進行回訪調查,每個用戶在到此店維修或保養后可以對該店進行打分,最高分為10分.上個月公司對該4S店的100位到店維修保養的客戶進行了調查,將打分的客戶按所打分值分成以下幾組:
某汽車公司為了考查某4S店的服務態度,對到店維修保養的客戶進行回訪調查,每個用戶在到此店維修或保養后可以對該店進行打分,最高分為10分.上個月公司對該4S店的100位到店維修保養的客戶進行了調查,將打分的客戶按所打分值分成以下幾組:查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $({0,\frac{{4\sqrt{3}}}{3}}]$ | B. | $[{2,\frac{{4\sqrt{3}}}{3}}]$ | C. | $[{\frac{{4\sqrt{3}}}{3},+∞})$ | D. | [2,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}+\frac{{\sqrt{3}}}{4}$ | B. | $\frac{1}{2}-\frac{{\sqrt{3}}}{4}$ | C. | $\frac{3}{4}$ | D. | 0 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a>0 | B. | a≥0 | C. | $0<a≤\frac{2}{e}$ | D. | $0≤a≤\frac{2}{e}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com