
分析 (1)由條件根據正弦函數的對稱性,求得函數y=$\frac{1}{2}$sin(2x+$\frac{π}{6}$)-1的對稱軸和對稱中心.
(2)根據三角函數的單調性解答.
(3)根據x的取值范圍求得(2x+$\frac{π}{6}$)的取值范圍,然后由正弦函數圖象的性質求其值域.
解答 解:(1)對于函數y=$\frac{1}{2}$sin(2x+$\frac{π}{6}$)-1,令2x+$\frac{π}{6}$=kπ+$\frac{π}{2}$,k∈Z,
解得x=$\frac{kπ}{2}$+$\frac{π}{6}$,k∈Z,
故函數的對稱軸方程為x=$\frac{kπ}{2}$+$\frac{π}{6}$,k∈Z,
令2x+$\frac{π}{6}$=kπ,k∈Z,
解得x=$\frac{kπ}{2}$-$\frac{π}{12}$,k∈Z,
故函數的對稱中心是($\frac{kπ}{2}$-$\frac{π}{12}$,0),k∈Z.
(2)對于函數y=$\frac{1}{2}$sin(2x+$\frac{π}{6}$)-1,令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z.
解得kπ-$\frac{π}{3}$≤x≤kπ+$\frac{π}{6}$,k∈Z.
所以該函數的單調增區間是[kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],k∈Z.
令2kπ+$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$,k∈Z.
解得kπ+$\frac{π}{6}$≤x≤kπ+$\frac{2π}{3}$,k∈Z.
所以該函數的單調減區間是[kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$],k∈Z.
(3)∵x∈(-$\frac{π}{4}$,$\frac{π}{3}$),
∴2x+$\frac{π}{6}$∈(-$\frac{π}{3}$,$\frac{5π}{6}$),
∴y=$\frac{1}{2}$sin(2x+$\frac{π}{6}$)-1的值域是(-$\frac{\sqrt{3}+1}{4}$,$-\frac{1}{2}$).
點評 本題考查了正弦函數圖象的對稱性,單調性,屬于基礎題,熟記函數圖象性質即可解題.


 七星圖書口算速算天天練系列答案
七星圖書口算速算天天練系列答案科目:高中數學 來源: 題型:解答題
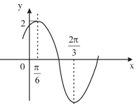 已知函數y=Asin(ωx+φ),(A>0,|φ|<π,ω>0)的一段圖象如圖所示.
已知函數y=Asin(ωx+φ),(A>0,|φ|<π,ω>0)的一段圖象如圖所示.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
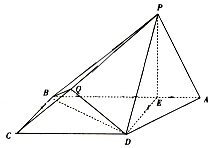 在四棱錐P-ABCD中,底面ABCD是梯形,AB⊥BC,BC⊥CD,點E是線段AB上的一點,DE⊥平面PAB,△ADE,為等腰直角三角形,DE=1,PE=2,AB=4,PA=$\sqrt{5}$.
在四棱錐P-ABCD中,底面ABCD是梯形,AB⊥BC,BC⊥CD,點E是線段AB上的一點,DE⊥平面PAB,△ADE,為等腰直角三角形,DE=1,PE=2,AB=4,PA=$\sqrt{5}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $[-\frac{3}{4},0)$ | B. | [-1,1) | C. | $[-\frac{1}{2},1)$ | D. | [-1,0) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (1,2] | B. | ($\frac{13}{4}$,2] | C. | (1,3] | D. | ($\frac{13}{4}$,3] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
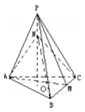 如圖所示,三棱錐P-ABC的高PO=8,AC=BC=3,∠ACB=30°,M,N分別在BC和PO上,且CM=x,PN=2x(x∈(0,3)),以下四個圖象大致描繪了三棱錐N-AMC的體積y與x的變化關系,其中正確的 是( )
如圖所示,三棱錐P-ABC的高PO=8,AC=BC=3,∠ACB=30°,M,N分別在BC和PO上,且CM=x,PN=2x(x∈(0,3)),以下四個圖象大致描繪了三棱錐N-AMC的體積y與x的變化關系,其中正確的 是( )| A. | 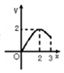 | B. |  | C. | 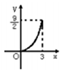 | D. | 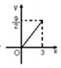 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
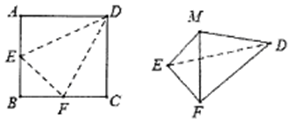
| A. | 2π | B. | 4π | C. | $\sqrt{6}$π | D. | 6π |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com