
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{15}}{5}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{\sqrt{3}}{3}$ |
分析 【解法一】設M、N、P分別為AB,BB1和B1C1的中點,得出AB1、BC1夾角為MN和NP夾角或其補角;根據中位線定理,結合余弦定理求出AC、MQ,MP和∠MNP的余弦值即可.
【解法二】通過補形的辦法,把原來的直三棱柱變成直四棱柱,解法更簡潔.
解答 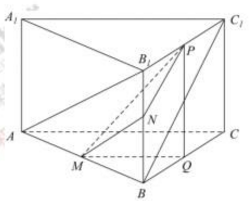 解:【解法一】如圖所示,設M、N、P分別為AB,BB1和B1C1的中點,
解:【解法一】如圖所示,設M、N、P分別為AB,BB1和B1C1的中點,
則AB1、BC1夾角為MN和NP夾角或其補角
(因異面直線所成角為(0,$\frac{π}{2}$]),
可知MN=$\frac{1}{2}$AB1=$\frac{\sqrt{5}}{2}$,
NP=$\frac{1}{2}$BC1=$\frac{\sqrt{2}}{2}$;
作BC中點Q,則△PQM為直角三角形;
∵PQ=1,MQ=$\frac{1}{2}$AC,
△ABC中,由余弦定理得
AC2=AB2+BC2-2AB•BC•cos∠ABC
=4+1-2×2×1×(-$\frac{1}{2}$)
=7,
∴AC=$\sqrt{7}$,
∴MQ=$\frac{\sqrt{7}}{2}$;
在△MQP中,MP=$\sqrt{{MQ}^{2}{+PQ}^{2}}$=$\frac{\sqrt{11}}{2}$;
在△PMN中,由余弦定理得
cos∠MNP=$\frac{{MN}^{2}{+NP}^{2}{-PM}^{2}}{2•MH•NP}$=$\frac{{(\frac{\sqrt{5}}{2})}^{2}{+(\frac{\sqrt{2}}{2})}^{2}{-(\frac{\sqrt{11}}{2})}^{2}}{2×\frac{\sqrt{5}}{2}×\frac{\sqrt{2}}{2}}$=-$\frac{\sqrt{10}}{5}$;
又異面直線所成角的范圍是(0,$\frac{π}{2}$],
∴AB1與BC1所成角的余弦值為$\frac{\sqrt{10}}{5}$.
【解法二】如圖所示,
補成四棱柱ABCD-A1B1C1D1,求∠BC1D即可;
BC1=$\sqrt{2}$,BD=$\sqrt{{2}^{2}{+1}^{2}-2×2×1×cos60°}$=$\sqrt{3}$,
C1D=$\sqrt{5}$,
∴${{BC}_{1}}^{2}$+BD2=${{C}_{1}D}^{2}$,
∴∠DBC1=90°,
∴cos∠BC1D=$\frac{\sqrt{2}}{\sqrt{5}}$=$\frac{\sqrt{10}}{5}$.
點評 本題考查了空間中的兩條異面直線所成角的計算問題,也考查了空間中的平行關系應用問題,是中檔題.


 探究與鞏固河南科學技術出版社系列答案
探究與鞏固河南科學技術出版社系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
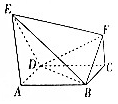 如圖,正方形ABCD的邊長為1,E,F是平面ABCD同一側的兩點,AE∥FC,AE⊥AB,AE=1,DE=$\sqrt{2}$,FC=$\frac{1}{2}$.
如圖,正方形ABCD的邊長為1,E,F是平面ABCD同一側的兩點,AE∥FC,AE⊥AB,AE=1,DE=$\sqrt{2}$,FC=$\frac{1}{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 隨機變量ξ,η滿足η=2ξ+3,則其方差的關系為D(η)=4D(ξ) | |
| B. | 回歸分析中,R2的值越大,說明殘差平方和越小 | |
| C. | 畫殘差圖時,縱坐標一定為殘差,橫坐標一定為編號 | |
| D. | 回歸直線一定過樣本點中心 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com