
【題目】某高校共有15000人,其中男生10500人,女生4500人,為調查該校學生每周平均體育運動時間的情況,采用分層抽樣的方法,收集300位學生每周平均體育運動時間的樣本數據(單位:小時)
(1)應收集多少位女生樣本數據?
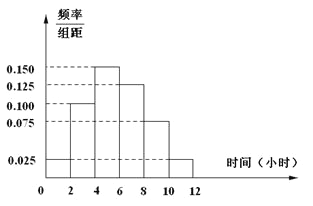
(2)根據這300個樣本數據,得到學生每周平均體育運動時間的頻率分布直方圖(如圖所示),其中樣本數據分組區間為:![]() .估計該校學生每周平均體育運動時間超過4個小時的概率.
.估計該校學生每周平均體育運動時間超過4個小時的概率.
(3)在樣本數據中,有60位女生的每周平均體育運動時間超過4個小時.請完成每周平均體育運動時間與性別的列聯表,并判斷是否有![]() 的把握認為“該校學生的每周平均體育運動時間與性別有關”.
的把握認為“該校學生的每周平均體育運動時間與性別有關”.
附:
![]()
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
【答案】(1)90;(2)0.75;(3)有![]() 的把握認為“該校學生的每周平均體育運動時間與性別有關”.
的把握認為“該校學生的每周平均體育運動時間與性別有關”.
【解析】
試題分析:(1)利用分層抽樣的應用可以算出![]() ,記應收集90位女生的樣本數據.(2)根據頻率分布直方圖可得
,記應收集90位女生的樣本數據.(2)根據頻率分布直方圖可得![]() .(3)根據題意300位學生中有
.(3)根據題意300位學生中有![]() 人的每周平均體育運動時間超過4小時,75人的每周平均體育運動時間不超過4小時.又因為樣本數據中有210份是關于男生的,90份是關于女生的.可以畫出每周平均體育運動時間與性別列聯表,計算
人的每周平均體育運動時間超過4小時,75人的每周平均體育運動時間不超過4小時.又因為樣本數據中有210份是關于男生的,90份是關于女生的.可以畫出每周平均體育運動時間與性別列聯表,計算![]() .則有
.則有![]() 的把握認為“該校學生的每周平均體育運動時間與性別有關”.
的把握認為“該校學生的每周平均體育運動時間與性別有關”.
(1)![]() ,所以應收集90位女生的樣本數據.
,所以應收集90位女生的樣本數據.
由頻率分布直方圖得![]() ,該校學生每周平均體育運動時間超過4個小時的概率為
,該校學生每周平均體育運動時間超過4個小時的概率為![]() .
.
由(2)知,300位學生中有![]() 人的每周平均體育運動時間超過4小時,75人的每周平均體育運動時間不超過4小時.又因為樣本數據中有210份是關于男生的,90份是關于女生的.所以每周平均體育運動時間與性別列聯表如下:
人的每周平均體育運動時間超過4小時,75人的每周平均體育運動時間不超過4小時.又因為樣本數據中有210份是關于男生的,90份是關于女生的.所以每周平均體育運動時間與性別列聯表如下:
每周平均體育運動時間與性別列聯表
男生 | 女生 | 總計 | |
每周平均體育運動時間不超過4小時 | 45 | 30 | 75 |
每周平均體育運動時間超過4小時 | 165 | 60 | 225 |
總計 | 210 | 90 | 300 |
結合列聯表可算得![]() .
.
有![]() 的把握認為“該校學生的每周平均體育運動時間與性別有關”.
的把握認為“該校學生的每周平均體育運動時間與性別有關”.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】如圖,在邊長為6的正方形![]() 中,弧
中,弧![]() 的圓心為
的圓心為![]() ,過弧
,過弧![]() 上的點
上的點![]() 作弧
作弧![]() 的切線,與
的切線,與![]() 、
、![]() 分別相交于點
分別相交于點![]() 、
、![]() ,
,![]() 的延長線交
的延長線交![]() 邊于點
邊于點![]() .
.
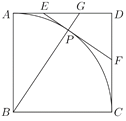
(1)設![]() ,
,![]() ,求
,求![]() 與
與![]() 之間的函數解析式,并寫出函數定義域;
之間的函數解析式,并寫出函數定義域;
(2)當![]() 時,求
時,求![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】足球,有“世界第一運動的美譽,是全球體育界最具影響力的單項體育運動之一.足球傳球是足球運動技術之一,是比賽中組織進攻、組織戰術配合和進行射門的主要手段.足球截球也是足球運動技術的一種,是將對方控制或傳出的球占為己有,或破壞對方對球的控制的技術,是比賽中由守轉攻的主要手段.這兩種運動技術都需要球運動員的正確判斷和選擇.現有甲、乙兩隊進行足球友誼賽,A、B兩名運動員是甲隊隊員,C是乙隊隊員,B在A的正西方向,A和B相距20m,C在A的正北方向,A和C相距14![]() m.現A沿北偏西60°方向水平傳球,球速為10
m.現A沿北偏西60°方向水平傳球,球速為10![]() m/s,同時B沿北偏西30°方向以10m/s的速度前往接球,C同時也以10m/s的速度前去截球.假設球與B、C都在同一平面運動,且均保持勻速直線運動.
m/s,同時B沿北偏西30°方向以10m/s的速度前往接球,C同時也以10m/s的速度前去截球.假設球與B、C都在同一平面運動,且均保持勻速直線運動.
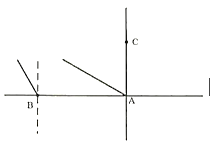
(1)若C沿南偏西60°方向前去截球,試判斷B能否接到球?請說明理由.
(2)若C改變(1)的方向前去截球,試判斷C能否球成功?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=2cos2x﹣cos(2x﹣![]() ).
).
(1)求f(x)的周期和最大值;
(2)已知△ABC中,角A.B.C的對邊分別為A,B,C,若f(π﹣A)=![]() ,b+c=2,求a的最小值.
,b+c=2,求a的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從甲、乙兩名學生中選拔一人參加射箭比賽,為此需要對他們的射箭水平進行測試.現這兩名學生在相同條件下各射箭10次,命中的環數如下:
甲 | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
乙 | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(1)計算甲、乙兩人射箭命中環數的平均數和標準差;
(2)比較兩個人的成績,然后決定選擇哪名學生參加射箭比賽.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下圖中的幾何體是由兩個有共同底面的圓錐組成.已知兩個圓錐的頂點分別為P、Q,高分別為2、1,底面半徑為1.A為底面圓周上的定點,B為底面圓周上的動點(不與A重合).下列四個結論:
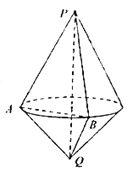
①三棱錐![]() 體積的最大值為
體積的最大值為![]() ;
;
②直線PB與平面PAQ所成角的最大值為![]() ;
;
③當直線BQ與AP所成角最小時,其正弦值為![]() ;
;
④直線BQ與AP所成角的最大值為![]() ;
;
其中正確的結論有___________.(寫出所有正確結論的編號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,定義域為![]() 上的函數
上的函數![]() 是由一條射線及拋物線的一部分組成.利用該圖提供的信息解決下面幾個問題.
是由一條射線及拋物線的一部分組成.利用該圖提供的信息解決下面幾個問題.

(1)求![]() 的解析式;
的解析式;
(2)若![]() 關于的方程
關于的方程![]() 有三個不同解,求
有三個不同解,求![]() 的取值范圍;
的取值范圍;
(3)若![]() ,求
,求![]() 的取值集合.
的取值集合.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中,假命題為( )
A.存在四邊相等的四邊形不是正方形
B.z1 , z2∈C,z1+z2為實數的充分必要條件是z1 , z2互為共軛復數
C.若x,y∈R,且x+y>2,則x,y至少有一個大于1
D.對于任意n∈N* , ![]() +
+ ![]() +…+
+…+ ![]() 都是偶數
都是偶數
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com