
分析 設P(x,y),表示出|PA|2+|PF|2,利用導數求最值.
解答 解:設P(x,y),則
t=|PA|2+|PF|2=(x-5)2+(y-2$\sqrt{2}$)2+(x-1)2+y2=(x2-10x+25)+(4x-4$\sqrt{2}$$•2\sqrt{x}$+8)+(x2-2x+1)+4x
=2x2-4x+34-4$\sqrt{2}$$•2\sqrt{x}$,
∴t′=4x-4-$\frac{4\sqrt{2}}{\sqrt{x}}$,
函數在(0,2)上單調遞減,(2,+∞)上單調遞增,
∴x=2時,函數取得最小值18,
故答案為:18.
點評 本題考查直線與拋物線的位置關系,考查導數知識的運用,正確求出|PA|2+|PF|2是關鍵.


 百年學典課時學練測系列答案
百年學典課時學練測系列答案 仁愛英語同步練習冊系列答案
仁愛英語同步練習冊系列答案科目:高中數學 來源: 題型:選擇題
| A. | {x|1<x≤2} | B. | {x|1≤x≤2} | C. | {x|x<1} | D. | {x|-2≤x<1} |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,公路AM、AN圍成的是一塊頂角為α的角形耕地,其中tanα=-2.在該塊土地中P處有一小型建筑,經測量,它到公路AM,AN的距離分別為3km,$\sqrt{5}$km.現要過點P修建一條直線公路BC,將三條公路圍成的區域ABC建成一個工業園.
如圖,公路AM、AN圍成的是一塊頂角為α的角形耕地,其中tanα=-2.在該塊土地中P處有一小型建筑,經測量,它到公路AM,AN的距離分別為3km,$\sqrt{5}$km.現要過點P修建一條直線公路BC,將三條公路圍成的區域ABC建成一個工業園.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(x)的最小正周期為2π | B. | f(x)在[-$\frac{π}{2}$,$\frac{π}{2}$]內單調遞增 | ||
| C. | f(x)的圖象關于(-$\frac{π}{2}$,0)對稱 | D. | f(x)的圖象關于x=$\frac{π}{8}$對稱 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
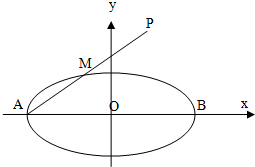 已知橢圓C;$\frac{x^2}{4}+\frac{y^2}{b}$=1(0<b<4)的左右頂點分別為A、B,M為橢圓上的任意一點,A關于M的對稱點為P,如圖所示,
已知橢圓C;$\frac{x^2}{4}+\frac{y^2}{b}$=1(0<b<4)的左右頂點分別為A、B,M為橢圓上的任意一點,A關于M的對稱點為P,如圖所示,查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com