
 某工廠生產A,B兩種型號的產品,每種型號的產品在出廠時按質量分為一等品和二等品,為便于掌握生產狀況,質檢時將產品分為每20件一組,分別記錄每組一等品的件數.現隨機抽取了5組的質檢記錄,其一等品數莖葉圖如圖所示:
某工廠生產A,B兩種型號的產品,每種型號的產品在出廠時按質量分為一等品和二等品,為便于掌握生產狀況,質檢時將產品分為每20件一組,分別記錄每組一等品的件數.現隨機抽取了5組的質檢記錄,其一等品數莖葉圖如圖所示: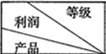 | 一等品 | 二等品 |
| A型 | 4(萬元) | 3(萬元) |
| B型 | 3(萬元) | 2(萬元) |
分析 (1)根據所給的產品的總數和由莖葉圖知每一種一等品的件數,得到A、B兩種產品為一等品的概率.
(2)根據表一所給的利潤,結合莖葉圖求出變量對應的概率,寫出分布列,求出期望值.
解答 解:(1)根據所給的產品的總數和由莖葉圖知每一種一等品的件數,
得到A、B兩種產品為一等品的概率,PA=$\frac{9+12+13+17+17}{100}$=0.68;PB=$\frac{8+16+14+13+20}{100}$=0.71.
(2)∵P(ξ=4)=0.68,P(ξ=3)=0.32,
P(η=3)=0.71,P(η=2)=0.29.
∴隨機變量ξ、η的分布列
| ξ | 4 | 3 |
| P | 0.68 | 0.32 |
| η | 3 | 2 |
| P | 0.71 | 0.29 |
點評 本題考查離散型隨機變量的分布列和期望、莖葉圖和表格,考查推理能力與計算能力,屬于中檔題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 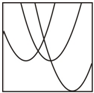 | B. | 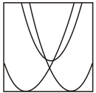 | C. | 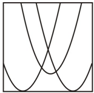 | D. |  |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [$\frac{1}{2},1$] | B. | [-1,-$\frac{1}{2}$] | C. | [$\frac{1}{2},1$) | D. | (-1,-$\frac{1}{2}$] |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com