
如圖, 和
和 所在平面互相垂直,且
所在平面互相垂直,且 ,
, ,E、F、G分別為AC、DC、AD的中點.
,E、F、G分別為AC、DC、AD的中點.
(1)求證: 平面BCG;
平面BCG;
(2)求三棱錐D-BCG的體積.
附:椎體的體積公式 ,其中S為底面面積,h為高.
,其中S為底面面積,h為高.
(1)詳見解析;(2)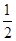
解析試題分析:(1)由已知得, 是
是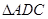 的中位線,故
的中位線,故 ,則可轉化為證明
,則可轉化為證明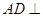 平面BCG.易證
平面BCG.易證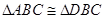 ,則有
,則有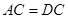 ,則在等腰三角形
,則在等腰三角形 和等腰三角形
和等腰三角形 中,且
中,且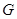 是
是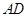 中點,故
中點,故 ,
,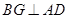 .從而
.從而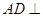 平面BCG,進而
平面BCG,進而 平面BCG;(2)求四面體體積,為了便于計算底面積和高,往往可采取等體積轉化法.由平面
平面BCG;(2)求四面體體積,為了便于計算底面積和高,往往可采取等體積轉化法.由平面 平面
平面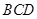 ,利用面面垂直的性質,易作出面
,利用面面垂直的性質,易作出面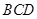 的垂線,同時求出點
的垂線,同時求出點 到面
到面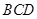 的距離,從而可求出點
的距離,從而可求出點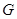 到平面
到平面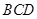 距離,即四面體
距離,即四面體 的高,進而求四面體體積.
的高,進而求四面體體積.
(1)證明:由已知得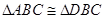 .因此
.因此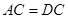 .又
.又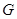 為
為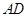 中點,所以
中點,所以 ;同理
;同理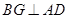 ;因此
;因此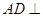 平面
平面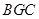 .又
.又 .所以
.所以 平面BCG.
平面BCG.
(2)在平面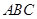 內.作
內.作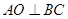 .交
.交 延長線于
延長線于 .由平面
.由平面 平面
平面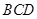 .知
.知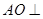 平面
平面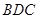 .
.
又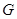 為
為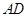 中點,因此
中點,因此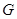 到平面
到平面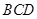 距離
距離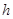 是
是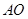 長度的一半.在
長度的一半.在 中,
中, .
.
所以 .
.
考點:1、直線和平面垂直的判定;2、面面垂直的性質;3、四面體的體積.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
如圖,點 為斜三棱柱
為斜三棱柱 的側棱
的側棱 上一點,
上一點,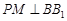 交
交 于點
于點 ,
, 交
交 于點
于點 .
.
(1) 求證: ;
;
(2) 在任意 中有余弦定理:
中有余弦定理: .
.
拓展到空間,類比三角形的余弦定理,寫出斜三棱柱的三個側面面積與其中兩個側面所成的二面角之間的關系式,并予以證明
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在幾何體ABCDE中,∠BAC= ,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1.
,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1.
(1)設平面ABE與平面ACD的交線為直線 ,求證:
,求證: ∥平面BCDE;
∥平面BCDE;
(2)設F是BC的中點,求證:平面AFD⊥平面AFE;
(3)求幾何體ABCDE的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,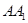 ,
, 為圓柱
為圓柱 的母線,
的母線, 是底面圓
是底面圓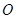 的直徑,
的直徑,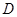 ,
,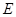 分別是
分別是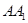 ,
,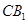 的中點,
的中點,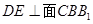 .
.
(1)證明: ;
;
(2)證明: ;
;
(3)假設這是個大容器,有條體積可以忽略不計的小魚能在容器的任意地方游弋,如果魚游到四棱錐 內會有被捕的危險,求魚被捕的概率.
內會有被捕的危險,求魚被捕的概率.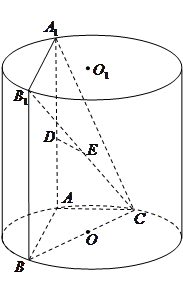
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(2013•浙江)如圖,在四棱錐P﹣ABCD中,PA⊥面ABCD,AB=BC=2,AD=CD= ,PA=
,PA= ,∠ABC=120°,G為線段PC上的點.
,∠ABC=120°,G為線段PC上的點.
(Ⅰ)證明:BD⊥平面PAC;
(Ⅱ)若G是PC的中點,求DG與PAC所成的角的正切值;
(Ⅲ)若G滿足PC⊥面BGD,求 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com