
分析 先根據題目的條件建立關于a、b、c的關系式,再結合基本不等式求出最小即可,注意等號成立的條件.
解答 解:∵f(x)=ax2+bx+c
∴f′(x)=2ax+b,f′(0)=b>0
∵對任意實數x都有f(x)≥0
∴a>0,c>0,b2-4ac≤0即 $\frac{4ac}{{b}^{2}}$≥1
則 $\frac{f(1)}{f′(0)}$=$\frac{a+b+c}{b}$=1+$\frac{a+c}{b}$,
而($\frac{a+c}{b}$)2=$\frac{{a}^{2}{+c}^{2}+2ac}{{b}^{2}}$≥$\frac{4ac}{{b}^{2}}$≥1,
∴$\frac{f(1)}{f′(0)}$=$\frac{a+b+c}{b}$=1+$\frac{a+c}{b}$≥2,
故答案為:2.
點評 本題主要考查了導數的運算,以及函數的最值及其幾何意義和不等式的應用,屬于中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
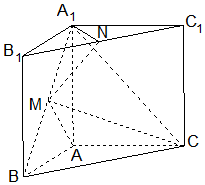 在三棱柱ABC-A1B1C1中,側棱與底面垂直,∠BAC=90°,AB=AA1,點M,N分別為A1B 和B1C1的中點.
在三棱柱ABC-A1B1C1中,側棱與底面垂直,∠BAC=90°,AB=AA1,點M,N分別為A1B 和B1C1的中點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com