
| A. | 函數f(x)的最小正周期為2π | |
| B. | f(x)在[$\frac{5π}{8}$,$\frac{9π}{8}$]單調遞減 | |
| C. | f(x)的圖象關于直線x=-$\frac{π}{6}$對稱 | |
| D. | 將f(x)的圖象向右平移$\frac{π}{8}$,再向下平移$\frac{1}{2}$個單位長度后會得到一個奇函數的圖象 |
分析 化函數f(x)為正弦型函數,再判斷選項中的命題是否正確.
解答 解:函數f(x)=(sinx+cosx)cosx
=sinxcosx+cos2x
=$\frac{1}{2}$sin2x+$\frac{1+cos2x}{2}$
=$\frac{\sqrt{2}}{2}$($\frac{\sqrt{2}}{2}$sin2x+$\frac{\sqrt{2}}{2}$cos2x)+$\frac{1}{2}$
=$\frac{\sqrt{2}}{2}$sin(2x+$\frac{π}{4}$)+$\frac{1}{2}$,
∴f(x)的最小正周期為T=$\frac{2π}{ω}$=π,∴A錯誤;
x∈[$\frac{5π}{8}$,$\frac{9π}{8}$]時,2x+$\frac{π}{4}$∈[$\frac{3π}{2}$,$\frac{5π}{2}$],
f(x)是單調遞增函數,∴B錯誤;
當x=-$\frac{π}{6}$時,f(x)=$\frac{\sqrt{2}}{2}$sin(-$\frac{π}{3}$+$\frac{π}{4}$)+$\frac{1}{2}$=$\frac{\sqrt{2}}{2}$sin(-$\frac{π}{12}$)+$\frac{1}{2}$,
∴x=-$\frac{π}{6}$不是f(x)的對稱軸,C錯誤;
將f(x)的圖象向右平移$\frac{π}{8}$,得y=$\frac{\sqrt{2}}{2}$sin2[(x-$\frac{π}{8}$)+$\frac{π}{4}$]+$\frac{1}{2}$的圖象,
再向下平移$\frac{1}{2}$個單位長度得y=$\frac{\sqrt{2}}{2}$sin2x的圖象,它是奇函數,D正確.
故選:D.
點評 本題考查了命題真假的判斷問題,也考查了三角函數的圖象與性質的應用問題,是中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | 3 | B. | $\frac{9\sqrt{3}}{2}$ | C. | $\frac{3\sqrt{3}}{2}$ | D. | 3$\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,在多面體ABCDEF中,四邊形ABCD為等腰梯形,AB∥CD,AB=4,CD=2,AC與BD交于O,且AC⊥BD,矩形ACEF⊥底面ABCD,M為EF上一動點,滿足$\overrightarrow{EM}$=λ$\overrightarrow{EF}$.
如圖,在多面體ABCDEF中,四邊形ABCD為等腰梯形,AB∥CD,AB=4,CD=2,AC與BD交于O,且AC⊥BD,矩形ACEF⊥底面ABCD,M為EF上一動點,滿足$\overrightarrow{EM}$=λ$\overrightarrow{EF}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (1,2) | B. | [1,2] | C. | (1,3) | D. | (1,$\frac{3}{2}$) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,$\frac{1}{e}$+1] | B. | (-∞,$\frac{1}{e}$+1) | C. | ($\frac{1}{e}$+1,+∞) | D. | ($\frac{1}{e}$,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
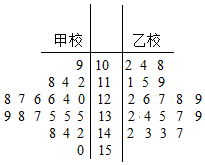
 一次數學考試后,某老師從自己所帶的兩個班級中各抽取6人,記錄他們的考試成績,得到如圖所示的莖葉圖.已知甲班6名同學成績的平均數為82,乙班6名同學成績的中位數為77,則x-y=( )
一次數學考試后,某老師從自己所帶的兩個班級中各抽取6人,記錄他們的考試成績,得到如圖所示的莖葉圖.已知甲班6名同學成績的平均數為82,乙班6名同學成績的中位數為77,則x-y=( )| A. | 3 | B. | -3 | C. | 4 | D. | -4 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 某市在對高三學生的4月理科數學調研測試的數據統計顯示,全市10000名學生的成績服從正態分布X~N(110,144),現從甲校100分以上的200份試卷中用系統抽樣的方法抽取了20份試卷來分析,統計如下:
某市在對高三學生的4月理科數學調研測試的數據統計顯示,全市10000名學生的成績服從正態分布X~N(110,144),現從甲校100分以上的200份試卷中用系統抽樣的方法抽取了20份試卷來分析,統計如下:| 試卷編號 | n1 | n2 | n3 | n4 | n5 | n6 | n7 | n8 | n9 | n10 |
| 試卷得分 | 109 | 118 | 112 | 114 | 126 | 128 | 127 | 124 | 126 | 120 |
| 試卷編號 | n11 | n12 | n13 | n14 | n15 | n16 | n17 | n18 | n19 | n20 |
| 試卷得分 | 135 | 138 | 135 | 137 | 135 | 139 | 142 | 144 | 148 | 150 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com