【題目】2019年4月10日21時整，全球六地（上海和臺北、布魯塞爾、圣地亞哥、東京和華盛頓同時召開新聞發布會，宣布人類首次利用虛擬射電望遠鏡，成功捕獲世界上首張黑洞圖像，公布的照片展示了一個中心為黑色的明亮環狀結構，看上去有點像個橙色的甜甜圈，其黑色部分是黑洞投下的“陰影”，明亮部分是繞黑洞高速旋轉的吸積盤.某同學作了一張黑洞示意圖，如圖所示，由兩個同心圓和半個同心圓環構成圓及圓環的半徑從內到外依次為2，3，4，5個單位在圖中隨機任取一點，則該點取自陰影的概率為（ ）
A.
B.
C.
D.
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，直線
的參數方程為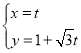
（
為參數），以坐標原點為極點，以
軸的正半軸為極軸建立極坐標系，曲線
的極坐標方程為
，直線與曲線相交于
兩點，與
軸相交于點
.
（1）求直線的普通方程和曲線的直角坐標方程；
（2）求
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】有限個元素組成的集合
，
，記集合
中的元素個數為
，即
.定義
，集合
中的元素個數記為
，當
時，稱集合具有性質
.
（1）
，
，判斷集合，
是否具有性質，并說明理由；
（2）設集合
，
且
(
)，若集合具有性質，求
的最大值；
（3）設集合，其中數列
為等比數列，
(
)且公比為有理數，判斷集合是否具有性質并說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，某校打算在長為1千米的主干道
一側的一片區域內臨時搭建一個強基計劃高校咨詢和宣傳臺，該區域由直角三角形區域
（
為直角）和以
為直徑的半圓形區域組成，點
（異于
，
）為半圓弧上一點，點
在線段上，且滿足
.已知
，設
，且
.初步設想把咨詢臺安排在線段
，
上，把宣傳海報懸掛在弧和線段上.
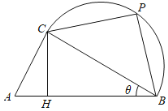
（1）若為了讓學生獲得更多的咨詢機會，讓更多的省內高校參展，打算讓
最大，求該最大值；
（2）若為了讓學生了解更多的省外高校，貼出更多高校的海報，打算讓弧和線段的長度之和最大，求此時的
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】折紙是一項藝術，可以折出很多數學圖形．將一張圓形紙片放在平面直角坐標系中，圓心B（－1，0），半徑為4，圓內一點A為拋物線
的焦點．若每次將紙片折起一角，使折起部分的圓弧的一點
始終與點A重合，將紙展平，得到一條折痕，設折痕與線段B的交點為P．
（Ⅰ）將紙片展平后，求點P的軌跡C的方程；
（Ⅱ）已知過點A的直線l與軌跡C交于R，S兩點，當l無論如何變動，在AB所在直線上存在一點T，使得
所在直線一定經過原點，求點T的坐標．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，要利用一半徑為
的圓形紙片制作三棱錐形包裝盒.已知該紙片的圓心為
，先以為中心作邊長為
（單位：
）的等邊三角形
，再分別在圓上取三個點
，
，
，使
，
，
分別是以
，
，
為底邊的等腰三角形.沿虛線剪開后，分別以，，為折痕折起，，，使得，，重合于點
，即可得到正三棱錐
.
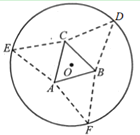
（1）若三棱錐是正四面體，求
的值；
（2）求三棱錐的體積
的最大值，并指出相應的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}的前n項和為Sn，a1＝1，an＞0，Sn2＝an+12﹣λSn+1，其中λ為常數.
（1）證明：Sn+1＝2Sn+λ；
（2）是否存在實數λ，使得數列{an}為等比數列，若存在，求出λ；若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓
，圓
，如圖，
分別交
軸正半軸于點
.射線
分別交于點
，動點
滿足直線
與
軸垂直，直線
與軸垂直.
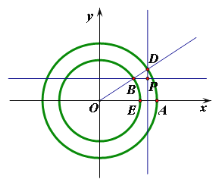
（1）求動點的軌跡
的方程；
（2）過點
作直線
交曲線與點
，射線
與點
，且交曲線于點
.問：
的值是否是定值？如果是定值，請求出該定值；如果不是定值，請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
