
【題目】折紙是一項藝術,可以折出很多數學圖形.將一張圓形紙片放在平面直角坐標系中,圓心B(-1,0),半徑為4,圓內一點A為拋物線![]() 的焦點.若每次將紙片折起一角,使折起部分的圓弧的一點
的焦點.若每次將紙片折起一角,使折起部分的圓弧的一點![]() 始終與點A重合,將紙展平,得到一條折痕,設折痕與線段
始終與點A重合,將紙展平,得到一條折痕,設折痕與線段![]() B的交點為P.
B的交點為P.
(Ⅰ)將紙片展平后,求點P的軌跡C的方程;
(Ⅱ)已知過點A的直線l與軌跡C交于R,S兩點,當l無論如何變動,在AB所在直線上存在一點T,使得![]() 所在直線一定經過原點,求點T的坐標.
所在直線一定經過原點,求點T的坐標.
【答案】(Ⅰ)軌跡C的方程為![]() ;(Ⅱ)點T的坐標為(4,0).
;(Ⅱ)點T的坐標為(4,0).
【解析】
(Ⅰ)依題意知PA=P![]() ,P的軌跡是以B、A為焦點,長軸長為4,焦距為2的橢圓,由題意能求出其橢圓方程;(Ⅱ)題意等價于在AB所在直線上存在一點T,使得TS與TR所在直線關于x軸對稱,當直線l垂直于x軸時,x軸上任意一點都滿足TS與TR所在直線關于x軸對稱,當直線l不垂直于x軸時,假設存在T(t,0)滿足條件,設l的方程為y=k(x﹣1),R(x1,y1),S(x2,y2),聯立
,P的軌跡是以B、A為焦點,長軸長為4,焦距為2的橢圓,由題意能求出其橢圓方程;(Ⅱ)題意等價于在AB所在直線上存在一點T,使得TS與TR所在直線關于x軸對稱,當直線l垂直于x軸時,x軸上任意一點都滿足TS與TR所在直線關于x軸對稱,當直線l不垂直于x軸時,假設存在T(t,0)滿足條件,設l的方程為y=k(x﹣1),R(x1,y1),S(x2,y2),聯立![]() ,得(3+4k2)x2﹣8k2x+4k2﹣12=0,由此利用根與系數的關系、根的判別式、直線關于x軸對稱,結合已知條件能求出存在T(4,0),使得當l變化時,總有TS與TR所在直線關于x軸對稱.
,得(3+4k2)x2﹣8k2x+4k2﹣12=0,由此利用根與系數的關系、根的判別式、直線關于x軸對稱,結合已知條件能求出存在T(4,0),使得當l變化時,總有TS與TR所在直線關于x軸對稱.
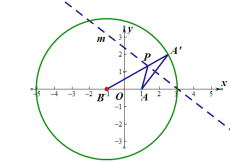
(Ⅰ)依題意:折痕所在直線m為線段![]() 的垂直平分線,∴PA=P
的垂直平分線,∴PA=P![]() ,
,
∴PB+PA= PB + P![]() =4>2,
=4>2,
∴P的軌跡是以B、A為焦點,長軸長為4,焦距為2的橢圓.
∴b2=3.
∴橢圓方程為![]() .
.
(Ⅱ)由題意可知:在AB所在直線上存在一點T,使得![]() 所在直線一定經過原點等價于在AB所在直線上存在一點T,使得TS與TR所在直線關于x軸對稱
所在直線一定經過原點等價于在AB所在直線上存在一點T,使得TS與TR所在直線關于x軸對稱
當直線l垂直于x軸時,x軸上任意一點都滿足TS與TR所在直線關于x軸對稱,
當直線l不垂直于x軸時,假設存在T(t,0)滿足條件,
設l的方程為y=k(x﹣1),R(x1,y1),S(x2,y2),
聯立![]() ,得(3+4k2)x2﹣8k2x+4k2﹣12=0,
,得(3+4k2)x2﹣8k2x+4k2﹣12=0,
由根與系數的關系得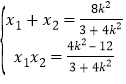 ,①,其中△>0,
,①,其中△>0,
∵TS與TR所在直線關于x軸對稱,∴![]() =0,②
=0,②
∵R,S兩點在直線y=k(x﹣1)上,
∴y1=k(x1﹣1),y2=k(x2﹣1),代入②,得:
![]() =
=![]() =0,
=0,
∴2x1x2﹣(t+1)(x1+x2)+2t=0,③
將①代入③,得![]() =
=![]() =0,④
=0,④
要使得④與k的取值無關,則t=4,
綜上所述,存在T(4,0),使得當l變化時,總有TS與TR所在直線關于x軸對稱,即在AB所在直線上存在一點T,使得![]() 所在直線一定經過原點.
所在直線一定經過原點.


科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系中,圓![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).以坐標原點為極點,
為參數).以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,直線
軸的正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求圓![]() 的普通方程和直線
的普通方程和直線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與圓
與圓![]() 交于
交于![]() 兩點,
兩點,![]() 是圓
是圓![]() 上不同于
上不同于![]() 兩點的動點,求
兩點的動點,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右頂點分別為
的左、右頂點分別為![]() ,
,![]() ,且以線段
,且以線段![]() 為直徑的圓與直線
為直徑的圓與直線![]() 相切,橢圓
相切,橢圓![]() 截直線
截直線![]() 所得線段的長度為1.
所得線段的長度為1.
(1)求橢圓![]() 的方程;
的方程;
(2)設過點![]() 的動直線
的動直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() ,
,![]() 兩點,若
兩點,若![]() (
(![]() 為坐標原點),求直線
為坐標原點),求直線![]() 的斜率的取值范圍.
的斜率的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
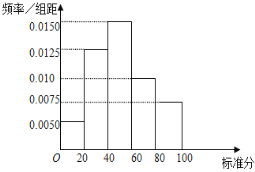
【題目】為了改善市民的生活環境,長沙某大型工業城市決定對長沙市的1萬家中小型化工企業進行污染情況摸排,并出臺相應的整治措施.通過對這些企業的排污口水質,周邊空氣質量等的檢驗,把污染情況綜合折算成標準分100分,發現長沙市的這些化工企業污染情況標準分基本服從正態分布N(50,162),分值越低,說明污染越嚴重;如果分值在[50,60]內,可以認為該企業治污水平基本達標.
(Ⅰ)如圖為長沙市的某工業區所有被調査的化工企業的污染情況標準分的頻率分布直方圖,請計算這個工業區被調査的化工企業的污染情況標準分的平均值,并判斷該工業區的化工企業的治污平均值水平是否基本達標;
(Ⅱ)大量調査表明,如果污染企業繼續生產,那么標準分低于18分的化工企業每月對周邊造成的直接損失約為10萬元,標準分在[18,34)內的化工企業每月對周邊造成的直接損失約為4萬元.長沙市決定關停80%的標準分低于18分的化工企業和60%的標準分在[18,34)內的化工企業,每月可減少的直接損失約有多少?
(附:若隨機變量![]() ,則
,則![]() ,
, ![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設a為實數,函數f(x)=ex﹣2x+2a,x∈R.
(1)求f(x)的單調區間及極值;
(2)求證:當a>ln2﹣1且x>0時,ex>x2﹣2ax+1.
查看答案和解析>>
科目:高中數學 來源: 題型:
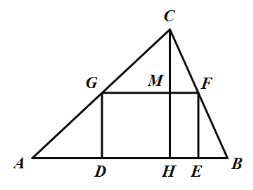
【題目】某市有一面積為12000平方米的三角形地塊![]() ,其中邊
,其中邊![]() 長為200米,現計劃建一個如圖所示的長方形停車場
長為200米,現計劃建一個如圖所示的長方形停車場![]() ,停車場的四個頂點都在
,停車場的四個頂點都在![]() 的三條邊上,其余的地面全部綠化.若建停車場的費用為180元/平方米,綠化的費用為60元/平方米,設
的三條邊上,其余的地面全部綠化.若建停車場的費用為180元/平方米,綠化的費用為60元/平方米,設![]() 米,建設工程的總費用為
米,建設工程的總費用為![]() 元.
元.
(1)求![]() 關于
關于![]() 的函數表達式:
的函數表達式:
(2)求停車場面積最大時![]() 的值,并求此時的工程總費用.
的值,并求此時的工程總費用.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com