
分析 分別設{an}公差為d,{bn}公比為q,通過整體運算把a3b3轉化為q的函數得答案.
解答 解:設{an}公差為d,{bn}公比為q,
由a1b1=1,a2b2=1,得a2b2=(a1+d)(b1q)=a1b1q+b1dq=q+b1dq=1,
∴b1dq=1-q,
${a}_{3}{b}_{3}=({a}_{1}+2d)({b}_{1}{q}^{2})$
=${a}_{1}{b}_{1}{q}^{2}+2d{b}_{1}{q}^{2}$=${q}^{2}+2d{b}_{1}{q}^{2}$
=${q}^{2}+2(d{b}_{1}q)•q={q}^{2}+2q(1-q)={q}^{2}+2q-2{q}^{2}$=-q2+2q=-(q-1)2+1≤1.
而q≠0,∴a3b3≠0,
∴a3b3∈(-∞,0)∪(0,1].
故答案為:(-∞,0)∪(0,1].
點評 本題考查等差數列和等比數列的通項公式,考查數學轉化思想方法,是中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
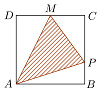 如圖所示,點P在邊長為1的正方形的邊上運動,設M是CD邊的中點,則當P沿著A-B-C-M運動時,以點P經過的路程x為自變量,三角形APM的面積為y,函數y=f(x)的圖象大致是( )
如圖所示,點P在邊長為1的正方形的邊上運動,設M是CD邊的中點,則當P沿著A-B-C-M運動時,以點P經過的路程x為自變量,三角形APM的面積為y,函數y=f(x)的圖象大致是( )| A. | 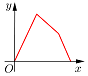 | B. | 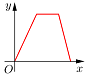 | C. | 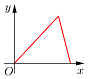 | D. |  |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$1 | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,0)點 | B. | ( $\overline{x}$,$\overline{y}$) 點 | C. | (0,$\overline{y}$)點 | D. | ( $\overline{x}$,0)點 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
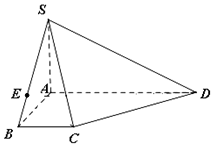 在如圖所示的四棱錐S-ABCD中,∠DAB=∠ABC=90°,SA=AB=BC=1,AD=3.
在如圖所示的四棱錐S-ABCD中,∠DAB=∠ABC=90°,SA=AB=BC=1,AD=3.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com