
分析 (Ⅰ)先求出函數的導函數令x的值為0代入其中得到f'(0)=-2即切線方程的斜率為-2,即可求出a的值,再利用導數和函數的最值的關系即可求出最小值,
(Ⅱ)求出函數的導函數,f(x)在區間(0,1)上無極值,則函數f(x)在(0,1)單調,分類討論,求出函數的單調性即可求出a的取值范圍
解答 解:(Ⅰ)因為$f(x)=\frac{ax+1}{e^x}$,所以$f'(x)=\frac{-ax+a-1}{e^x}$.
依題意,f′(0)=-2,解得a=-1.
所以$f(x)=\frac{-x+1}{e^x}$,$f'(x)=\frac{x-2}{e^x}$.
當x>2時,f'(x)>0,函數f(x)為增函數;
當x<2時,f'(x)<0,函數f(x)為減函數;
所以函數f(x)的最小值是$f(2)=-\frac{1}{e^2}$.
(Ⅱ)因為$f(x)=\frac{ax+1}{e^x}$,所以$f'(x)=\frac{-ax+a-1}{e^x}$.
(1)若a=0,則$f'(x)=-\frac{1}{e^x}<0$.此時f(x)在(0,1)上單調遞減,滿足條件.
(2)若a≠0,令f'(x)=0得$x=\frac{a-1}{a}=1-\frac{1}{a}$.
(ⅰ)若$1-\frac{1}{a}≤0$,即0<a≤1,則f'(x)<0在(0,1)上恒成立.
此時f(x)在(0,1)上單調遞減,滿足條件.
(ⅱ)若$0<1-\frac{1}{a}<1$,即a>1時,由f'(x)>0得$0<x<1-\frac{1}{a}$;
由f'(x)<0得$1-\frac{1}{a}<x<1$.
此時f(x)在$(0,1-\frac{1}{a})$上為增函數,在$(1-\frac{1}{a},1)$上為減,不滿足條件.
(ⅲ)若$1-\frac{1}{a}≥1$即a<0.則f'(x)<0在(0,1)上恒成立.
此時f(x)在(0,1)上單調遞減,滿足條件.
綜上,a≤1.
點評 考查學生利用導數求函數在閉區間上的最值的能力,以及導數和函數的單調性的關系,考查了分類討論的能力,屬于中檔題


 學練快車道口算心算速算天天練系列答案
學練快車道口算心算速算天天練系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
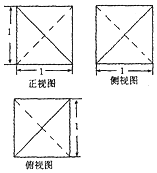
| A. | $\frac{1}{12}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com