
分析 (Ⅰ)當a=4時,把要解的不等式等價轉化為與之等價的三個不等式組,求出每個不等式組的解集,再取并集,即得所求.
(Ⅱ)利用絕對值三角不等式求得f(x)的最小值為|a-1|,再根據|a-1|≥5,求得a的取值范圍.
解答 解:(Ⅰ)當a=4時,求不等式f(x)≥6,即|x-1|+|x-a|=|x-1|+|x-4|≥6,
∴$\left\{\begin{array}{l}{x<1}\\{1-x+4-x≥6}\end{array}\right.$①,或$\left\{\begin{array}{l}{1≤x≤4}\\{x-1+4-x≥6}\end{array}\right.$ ②,或$\left\{\begin{array}{l}{x>4}\\{x-1+x-4≥6}\end{array}\right.$ ③.
解①求得x≤-$\frac{1}{2}$,解②求得x∈∅,解③求得 x≥$\frac{11}{2}$,
綜上可得,不等式的解集為{|x≤-$\frac{1}{2}$,或 x≥$\frac{11}{2}$}.
(Ⅱ)若f(x)≥5對x∈R恒成立,而f(x)=|x-1|+|x-a|≥|x-1-(x-a)|=|a-1|,
∴|a-1|≥5,即a-1≥5,或 a-1≤-5,求得a≥6,或 a≤-4.
點評 本題主要考查絕對值三角不等式,絕對值不等式的解法,函數的恒成立問題,體現了轉化、分類討論的數學思想,屬于中檔題.


 走進文言文系列答案
走進文言文系列答案科目:高中數學 來源: 題型:選擇題
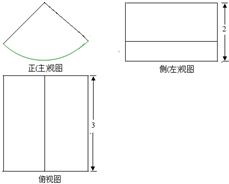 將一個質地均勻的幾何體放置在水平面上,其三視圖如圖所示,其中正(主)視圖是一個圓心角為90°的扇形,則該幾何體的表面積為( )
將一個質地均勻的幾何體放置在水平面上,其三視圖如圖所示,其中正(主)視圖是一個圓心角為90°的扇形,則該幾何體的表面積為( )| A. | 3π+6 | B. | 5π+6 | C. | 3π+12 | D. | 5π+12 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
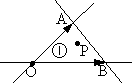 如圖,已知O,A,B是平面內不共線的三點,且$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,直線OA,OB,AB將平面區域分成7部分,若點P落在區域①中(含邊界),則z=2x+y的最大值為( )
如圖,已知O,A,B是平面內不共線的三點,且$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,直線OA,OB,AB將平面區域分成7部分,若點P落在區域①中(含邊界),則z=2x+y的最大值為( )| A. | 不存在 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,$\frac{1}{4}$) | B. | (0,$\frac{1}{2}$) | C. | (0,1) | D. | (0,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com