【題目】已知直角梯形
中，
是邊長為2的等邊三角形，
．沿
將
折起，使
至
處，且
；然后再將
沿
折起，使
至
處，且面
面
，
和
在面
的同側．
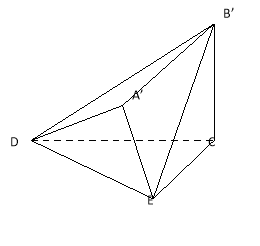
(Ⅰ) 求證：
平面
；
(Ⅱ) 求平面
與平面所構成的銳二面角的余弦值．
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】一個正方體的平面展開圖及該正方體的直觀圖的示意圖如圖所示.在正方體中，設BC的中點為M，GH的中點為N.
(1)請將字母F，G，H標記在正方體相應的頂點處(不需說明理由).
(2)判斷平面BEG與平面ACH的位置關系，并證明你的結論.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列給出的輸入語句、輸出語句和賦值語句：
（1）輸出語句INPUT 
，b，c
（2）輸入語句INPUT 
=3
（3）賦值語句3=A
（4）賦值語句A=B=C
則其中正確的個數是（ ）
（A）0 （B）1 （C）2 （D）3
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點(0,1),(3+2
,0),(3-2
,0)在圓C上.
(1)求圓C的方程.
(2)若圓C與直線x-y+a=0交于A,B兩點,且OA⊥OB,求a的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝x2＋
(x≠0，a∈R)．
(1)判斷函數f(x)的奇偶性；
(2)若f(x)在區間[2，＋∞)上是增函數，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
.
（1）當
時，求函數
在
上的最大值；
（2）令
，若
在區間
上為單調遞增函數，求
的取值范圍；
（3）當時，函數
的圖象與
軸交于兩點
且
，又
是
的導函數.若正常數
滿足條件
.證明：
<0.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】從某市主辦的科技知識競賽的學生成績中隨機選取了40名學生的成績作為樣本，已知這40名學生的成績全部在40分至100分之間，現將成績按如下方式分成6組，第一組
；第二組
；…；第六組
，并據此繪制了如圖所示的頻率分布直方圖．
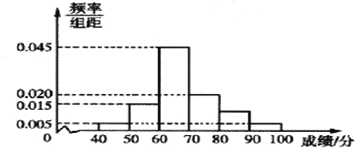
（1）求成績在區間
內的學生人數；
（2）從成績大于等于80分的學生中隨機選取2名，求至少有1名學生的成績在區間內的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
．
（1）當
時，求不等式
的解集；
（2）當
時，若對任意互不相等的實數
，都有
成立，求實數
的取值范圍；
（3）判斷函數
在
上的零點的個數，并說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
