
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時(shí),求函數(shù)
時(shí),求函數(shù)![]() 在
在![]() 上的最大值;
上的最大值;
(2)令![]() ,若
,若![]() 在區(qū)間
在區(qū)間![]() 上為單調(diào)遞增函數(shù),求
上為單調(diào)遞增函數(shù),求![]() 的取值范圍;
的取值范圍;
(3)當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 的圖象與
的圖象與![]() 軸交于兩點(diǎn)
軸交于兩點(diǎn)![]() 且
且![]() ,又
,又![]() 是
是![]() 的導(dǎo)函數(shù).若正常數(shù)
的導(dǎo)函數(shù).若正常數(shù)![]() 滿足條件
滿足條件![]() .證明:
.證明:![]() <0.
<0.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() ,理由見解析
,理由見解析
【解析】試題分析:(1)![]() ,可知
,可知![]() 在[
在[![]() ,1]是增函數(shù),在[1,2]是減函數(shù),所以最大值為f(1).(2)
,1]是增函數(shù),在[1,2]是減函數(shù),所以最大值為f(1).(2)![]() 在區(qū)間
在區(qū)間![]() 上為單調(diào)遞增函數(shù),即
上為單調(diào)遞增函數(shù),即![]() 在
在![]() 上恒成立。
上恒成立。![]() ,利用分離參數(shù)
,利用分離參數(shù)![]() 在
在![]() 上恒成立,即求
上恒成立,即求![]() 的最大值。
的最大值。
(3)![]() 有兩個(gè)實(shí)根
有兩個(gè)實(shí)根![]() ,
, ![]() ,兩式相減
,兩式相減![]() ,又
,又![]() ,
,![]()
![]() .要證:
.要證:![]() ,只需證:
,只需證:![]() ,令
,令![]() 可證。
可證。
試題解析:(1) ![]()
函數(shù)![]() ,1]是增函數(shù),在[1,2]是減函數(shù),
,1]是增函數(shù),在[1,2]是減函數(shù),
所以![]() .
.
(2)因?yàn)?/span>![]() ,所以
,所以![]() ,
,
因?yàn)?/span>![]() 在區(qū)間
在區(qū)間![]() 單調(diào)遞增函數(shù),所以
單調(diào)遞增函數(shù),所以![]() 在(0,3)恒成立
在(0,3)恒成立
![]() ,有
,有![]() =
=![]() ,(
,(![]() )
)
綜上:![]()
(3)∵![]() ,又
,又![]() 有兩個(gè)實(shí)根
有兩個(gè)實(shí)根![]() ,
,
∴![]() ,兩式相減,得
,兩式相減,得![]() ,
,
∴![]() ,
,
于是![]()
![]() .
.
![]()
要證:![]() ,只需證:
,只需證:![]()
只需證:![]() .(*)
.(*)
令![]() ,∴(*)化為
,∴(*)化為  ,只證
,只證![]() 即可.
即可.
![]() 在(0,1)上單調(diào)遞增,
在(0,1)上單調(diào)遞增,![]() ,
,
即![]() .∴
.∴![]() .
.
(其他解法根據(jù)情況酌情給分)


 字詞句篇與同步作文達(dá)標(biāo)系列答案
字詞句篇與同步作文達(dá)標(biāo)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
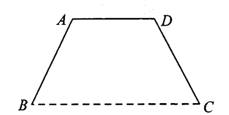
【題目】某單位將舉辦慶典活動(dòng),要在廣場(chǎng)上豎立一形狀為等腰梯形的彩門![]() (如圖).設(shè)計(jì)要求彩門的面積為
(如圖).設(shè)計(jì)要求彩門的面積為![]() (單位:
(單位:![]() ),高為
),高為![]() (單位:
(單位:![]() )(
)(![]() 為常數(shù)).彩門的下底
為常數(shù)).彩門的下底![]() 固定在廣場(chǎng)底面上,上底和兩腰由不銹鋼支架構(gòu)成,設(shè)腰和下底的夾角為
固定在廣場(chǎng)底面上,上底和兩腰由不銹鋼支架構(gòu)成,設(shè)腰和下底的夾角為![]() ,不銹鋼支架的長(zhǎng)度和記為
,不銹鋼支架的長(zhǎng)度和記為![]() .
.
(1)請(qǐng)將![]() 表示成關(guān)于
表示成關(guān)于![]() 的函數(shù)
的函數(shù)![]() ;
;
(2)問當(dāng)![]() 為何值
為何值![]() 最小,并求最小值.
最小,并求最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
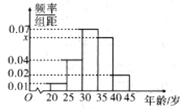
【題目】為創(chuàng)建全國(guó)文明城市,某區(qū)向各事業(yè)行政單位征集“文明過馬路”義務(wù)督導(dǎo)員.從符合條件的600名志愿者中隨機(jī)抽取100名,按年齡作分組如下:[20,25) , [25,30) , [30,35), [35,40) , [40,45] ,并得到如下頻率分布直方圖.
(Ⅰ)求圖中![]() 的值,并根據(jù)頻率分布直方圖統(tǒng)計(jì)這600名志愿者中年齡在[30.40)的人數(shù);
的值,并根據(jù)頻率分布直方圖統(tǒng)計(jì)這600名志愿者中年齡在[30.40)的人數(shù);
(Ⅱ)在抽取的100名志愿者中按年齡分層抽取10名參加區(qū)電視臺(tái)“文明伴你行”節(jié)目錄制,再?gòu)倪@10名志愿者中隨機(jī)選取3名到現(xiàn)場(chǎng)分享勸導(dǎo)制止行人闖紅燈的經(jīng)歷,記這3名志愿者中年齡不低于35歲的人數(shù)為![]() ,求
,求![]() 的分布列及數(shù)學(xué)期望.
的分布列及數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
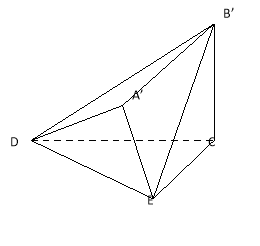
【題目】已知直角梯形![]() 中,
中,![]() 是邊長(zhǎng)為2的等邊三角形,
是邊長(zhǎng)為2的等邊三角形,![]() .沿
.沿![]() 將
將![]() 折起,使
折起,使![]() 至
至![]() 處,且
處,且![]() ;然后再將
;然后再將![]() 沿
沿![]() 折起,使
折起,使![]() 至
至![]() 處,且面
處,且面![]() 面
面![]() ,
,![]() 和
和![]() 在面
在面![]() 的同側(cè).
的同側(cè).

(Ⅰ) 求證:![]() 平面
平面![]() ;
;
(Ⅱ) 求平面![]() 與平面
與平面![]() 所構(gòu)成的銳二面角的余弦值.
所構(gòu)成的銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]()
![]() 的圖象過點(diǎn)
的圖象過點(diǎn)![]() 。
。
(1)求![]() 的值并求函數(shù)
的值并求函數(shù)![]() 的值域;
的值域;
(2)若關(guān)于![]() 的方程
的方程![]() 有實(shí)根,求實(shí)數(shù)
有實(shí)根,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(3)若函數(shù)![]() ,
, ![]() ,則是否存在實(shí)數(shù)
,則是否存在實(shí)數(shù)![]() ,使得函數(shù)
,使得函數(shù)![]() 的最大值為0?若存在,求出
的最大值為0?若存在,求出![]() 的值;若不存在,請(qǐng)說明理由。
的值;若不存在,請(qǐng)說明理由。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】有 ![]() 名男生,
名男生, ![]() 名女生,在下列不同條件下,求不同的排列方法種數(shù).(最后結(jié)果化成數(shù)
名女生,在下列不同條件下,求不同的排列方法種數(shù).(最后結(jié)果化成數(shù)
字)
(1)排成前后兩排,前排 ![]() 人,后排
人,后排 ![]() 人;
人;
(2)全體排成一排,甲不站在排頭也不站在排尾;
(3)全體排成一排,女生必須站在一起;
(4)全體排成一排,男生不能相鄰.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]()
(1)設(shè)![]() ,當(dāng)
,當(dāng)![]() 時(shí),求函數(shù)
時(shí),求函數(shù)![]() 的定義域,判斷并證明函數(shù)
的定義域,判斷并證明函數(shù)![]() 的奇偶性;
的奇偶性;
(2)是否存在實(shí)數(shù)![]() ,使得函數(shù)
,使得函數(shù)![]() 在
在![]() 遞減,并且最小值為1,若存在,求出
遞減,并且最小值為1,若存在,求出![]() 的值;若不存在,請(qǐng)說明理由.
的值;若不存在,請(qǐng)說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)試判斷函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)設(shè)![]() ,求
,求![]() 在
在![]() 上的最大值;
上的最大值;
(3)試證明:對(duì)任意![]() ,不等式
,不等式![]() 都成立(其中
都成立(其中![]() 是自然對(duì)數(shù)的底數(shù)).
是自然對(duì)數(shù)的底數(shù)).
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com