
【題目】已知函數![]() ,且
,且![]() .
.
(1)若函數![]() 在區間
在區間![]() 上是減函數,求實數
上是減函數,求實數![]() 的取值范圍;
的取值范圍;
(2)設函數![]() ,當
,當![]() 時,
時, ![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】甲、乙兩位學生參加數學競賽培訓,在培訓期間他們參加的5次預寒成績記錄如下:
甲:82,82,79,95,87
乙:95,75,80,90,85
(1)用莖葉圖表示這兩組數據;
(2)求甲、乙兩人成績的平均數與方差;
(3)若現要從中選派一人參加數學競賽,你認為選派哪位學生參加合適,說明理由?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的圖象關于直線
的圖象關于直線![]() 對稱.
對稱.
(1)求實數![]() 的值;
的值;
(2)若對任意的![]() ,使得
,使得![]() 有解,求實數
有解,求實數![]() 的取值范圍;
的取值范圍;
(3)若![]() 時,關于
時,關于![]() 的方程
的方程![]() 有四個不等式的實根,求實數
有四個不等式的實根,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠以![]() 千克/小時的速度勻速生產某種產品(生產條件要求
千克/小時的速度勻速生產某種產品(生產條件要求![]() ),每一小時可獲得的利潤是
),每一小時可獲得的利潤是![]() 元.
元.
(1)要使生產該產品2小時獲得的利潤不低于1500元,求![]() 的取值范圍;
的取值范圍;
(2) 要使生產480千克該產品獲得的利潤最大,問:該廠應該選取何種生產速度?并求此最大利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】脫貧是政府關注民生的重要任務,了解居民的實際收入狀況就顯得尤為重要.現從某地區隨機抽取![]() 個農戶,考察每個農戶的年收入與年積蓄的情況進行分析,設第
個農戶,考察每個農戶的年收入與年積蓄的情況進行分析,設第![]() 個農戶的年收入
個農戶的年收入![]() (萬元),年積蓄
(萬元),年積蓄![]() (萬元),經過數據處理得
(萬元),經過數據處理得![]()
(Ⅰ)已知家庭的年結余![]() 對年收入
對年收入![]() 具有線性相關關系,求線性回歸方程;
具有線性相關關系,求線性回歸方程;
(Ⅱ)若該地區的農戶年積蓄在![]() 萬以上,即稱該農戶已達小康生活,請預測農戶達到小康生活的最低年收入應為多少萬元?
萬以上,即稱該農戶已達小康生活,請預測農戶達到小康生活的最低年收入應為多少萬元?
附:在![]() 中,
中, 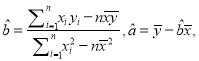 其中
其中![]() 為樣本平均值.
為樣本平均值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,
,![]() 、
、![]() 分別為左、右頂點,
分別為左、右頂點,![]() 為其右焦點,
為其右焦點,![]() 是橢圓
是橢圓![]() 上異于
上異于![]() 、
、![]() 的動點,且
的動點,且![]() 的最小值為-2.
的最小值為-2.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若過左焦點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,求
兩點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高二某班的一次數學測試成績的莖葉圖和頻率分布直方圖都受到不同程度的損壞,可見部分如下:

試著根據表中的信息解答下列問題:
(Ⅰ)求全班的學生人數及分數在[70,80)之間的頻數;
(Ⅱ)為快速了解學生的答題情況,老師按分層抽樣的方法從位于[70,80)和[80,90)分數段的試卷中抽取7份進行分析,再從中任選2人進行交流,求交流的學生中,成績位于[70,80)分數的人恰有一人被抽到的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校的一個社會實踐調查小組,在對該校學生的良好“用眼習慣”的調查中,隨機發放了120分問卷.對收回的100份有效問卷進行統計,得到如![]() 下列聯表:
下列聯表:
做不到科學用眼 | 能做到科學用眼 | 合計 | |
男 | 45 | 10 | 55 |
女 | 30 | 15 | 45 |
合計 | 75 | 25 | 100 |
(1)現按女生是否能做到科學用眼進行分層,從45份女生問卷中抽取了6份問卷,從這6份問卷中再隨機抽取3份,并記其中能做到科學用眼的問卷的份數![]() ,試求隨機變量
,試求隨機變量![]() 的分布列和數學期望;
的分布列和數學期望;
(2)若在犯錯誤的概率不超過![]() 的前提下認為良好“用眼習慣”與性別有關,那么根據臨界值表,最精確的
的前提下認為良好“用眼習慣”與性別有關,那么根據臨界值表,最精確的![]() 的值應為多少?請說明理由.
的值應為多少?請說明理由.
附:獨立性檢驗統計量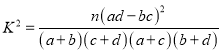 ,其中
,其中![]() .
.
獨立性檢驗臨界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 過點
過點 ,且離心率為
,且離心率為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若點![]() 與點
與點![]() 均在橢圓
均在橢圓![]() 上,且
上,且![]() 關于原點對稱,問:橢圓上是否存在點
關于原點對稱,問:橢圓上是否存在點![]() (點
(點![]() 在一象限),使得
在一象限),使得![]() 為等邊三角形?若存在,求出點
為等邊三角形?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com