
分析 運用橢圓的定義可得,點P的軌跡方程是$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1,把=-2x+3代入$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1,由判別式大于0,即可得出結論.
解答 解:由橢圓的定義可知,點P的軌跡是以M,N為焦點的橢圓,其方程是$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1,
把y=-2x+3代入$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1,并整理得,19x2-48x+24=0,由△=(-48)2-4×19×24>0,
∴在l上滿足|PM|+|PN|=4的點P有2個.
故答案為:2.
點評 本題考查了橢圓的定義及標準方程,考查了數學轉化思想方法及方程思想方法,解答此題的關鍵是把問題轉化為判斷直線方程與橢圓方程聯立的方程組是否有解,屬中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | {x|x≤2} | B. | {x|x>0} | C. | {x|x<0或x≥2} | D. | {x|0<x≤2} |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | |$\overrightarrow{b}$|=2 | B. | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | C. | $\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{1}{2}$ | D. | ($\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$)⊥$\overrightarrow{BC}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 25 | B. | 16 | C. | 10 | D. | 9 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
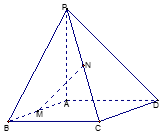 已知PA垂直于矩形ABCD所在平面,M,N分別是AB,PC的中點.
已知PA垂直于矩形ABCD所在平面,M,N分別是AB,PC的中點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com