【題目】已知橢圓
，直線
不經過橢圓上頂點
，與橢圓
交于
，
不同兩點.
（1）當
，
時，求橢圓的離心率的取值范圍；
（2）若
，直線
與
的斜率之和為
，證明：直線
過定點.
科目：高中數學 來源： 題型：
【題目】已知數列
的各項均為正數，
，且對任意
,都有
，數列前n項的和
.
（1）若數列是等比數列，求
的值和
；
（2）若數列是等差數列，求
和的關系式；
（3）
，當
時，求證: 
是一個常數.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司新發明了甲、乙兩種不同型號的手機，公司統計了消費者對這兩種型號手機的評分情況，作出如下的雷達圖，則下列說法不正確的是（ ）
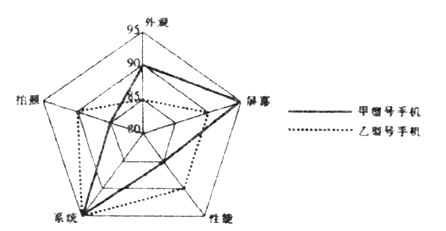
A. 甲型號手機在外觀方面比較好.B. 甲、乙兩型號的系統評分相同.
C. 甲型號手機在性能方面比較好.D. 乙型號手機在拍照方面比較好.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某興趣小組測量電視塔AE的高度H(單位m），如示意圖，垂直放置的標桿BC高度h=4m，仰角∠ABE=α，∠ADE=β
（1）該小組已經測得一組α、β的值，tanα=1.24,tanβ=1.20,,請據此算出H的值
（2）該小組分析若干測得的數據后，發現適當調整標桿到電視塔的距離d（單位m），使α與β之差較大，可以提高測量精確度，若電視塔實際高度為125m，問d為多少時，α-β最大
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨著我國經濟的高速發展，汽車的銷量也快速增加，每年因道路交通安全事故造成傷亡人數超過
萬人，根據國家質量監督檢驗檢疫局發布的《車輛駕駛人員血液、呼氣酒精含量閥值與檢驗》（
-醉駕車的測試
）的規定：飲酒駕車是指車輛駕駛人員血液中的酒精含量大于或者等于
，小于
的駕駛行為；醉酒駕車是指車輛駕駛人員血液中的酒精含量大于或者等于的駕駛行為，某市交通部門從
年飲酒后駕駛機動車輛發生交通事故的駕駛員中隨機抽查了
人進行統計，得到如下數據：
酒精含量
|
|
|
|
|
|
發生交通事故的人數 |
|
|
|
|
|
已知從這人中任意抽取兩人，兩人均是醉酒駕車的概率是
.
（1）求
，
的值；
（2）實踐證明，駕駛人員血液中的酒精含量與發生交通事故的人數具有線性相關性，試建立
關于
的線性回歸方程；
（3）試預測，駕駛人員血液中的酒精含量為多少時，發生交通事故的人數會超過取樣人數的
？
參考數據：
，
回歸直線方程
中系數計算公式
，
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為培養學生的閱讀習慣，某校開展了為期一年的“弘揚傳統文化，閱讀經典名著”活動. 活動后，為了解閱讀情況，學校統計了甲、乙兩組各10名學生的閱讀量（單位：本），統計結果用莖葉圖記錄如下，乙組記錄中有一個數據模糊，無法確認，在圖中以a表示.
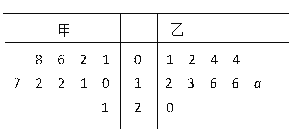
（Ⅰ）若甲組閱讀量的平均值大于乙組閱讀量的平均值，求圖中a的所有可能取值；
（Ⅱ）將甲、乙兩組中閱讀量超過15本的學生稱為“閱讀達人”. 設
，現從所有的“閱讀達人”里任取2人，求至少有1人來自甲組的概率；
（Ⅲ）記甲組閱讀量的方差為
. 若在甲組中增加一個閱讀量為10的學生，并記新得到的甲組閱讀量的方差為
，試比較，的大小.（結論不要求證明）
（注：
，其中
為數據
的平均數）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列命題正確的是（ ）
A.“若x＝3，則x2﹣2x﹣3＝0”的否命題是：“若x＝3，則x2﹣2x﹣3≠0”
B.在△ABC中，“A＞B”是“sinA＞sinB”的充要條件
C.若p∧q為假命題，則p∨q一定為假命題
D.“存在x0∈R，使得ex0≤0”的否定是：不存在x0∈R，使得e
0”
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某地隨著經濟的發展，居民收入逐年增長，下表是該地一建設銀行連續五年的儲蓄存款（年底余額），如下表1：
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
儲蓄存款y（千億元） | 5 | 6 | 7 | 8 | 10 |
為了研究計算的方便，工作人員將上表的數據進行了處理， 
得到下表2：
時間代號t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
（Ⅰ）求z關于t的線性回歸方程；
（Ⅱ）用所求回歸方程預測到2020年年底，該地儲蓄存款額可達多少？
（附：對于線性回歸方程
，其中
）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
