
【題目】在四棱錐![]() 中,
中,![]() ,
,![]() 分別為側棱
分別為側棱![]() ,
,![]() 的中點,則四面體
的中點,則四面體![]() 的體積與四棱錐
的體積與四棱錐![]() 的體積之比為___________
的體積之比為___________
【答案】![]()
【解析】
棱錐![]() 的體積可以看成四棱錐
的體積可以看成四棱錐![]() 的體積減去角上的四個小棱錐的體積得到,由
的體積減去角上的四個小棱錐的體積得到,由![]() 分別為側棱
分別為側棱![]() 的中點,得到棱錐
的中點,得到棱錐![]() 的體積與棱錐
的體積與棱錐![]() 的體積和為四棱錐
的體積和為四棱錐![]() 的體積的
的體積的![]() ;棱錐
;棱錐![]() 的體積與棱錐
的體積與棱錐![]() 的體積和為四棱錐
的體積和為四棱錐![]() 的體積的
的體積的![]() ,由此可得答案.
,由此可得答案.
解:∵如圖,棱錐![]() 的體積可以看成是四棱錐
的體積可以看成是四棱錐![]() 的體積減去角上的四個小棱錐的體積得到,
的體積減去角上的四個小棱錐的體積得到,
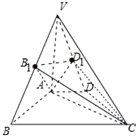
∵![]() 分別為側棱
分別為側棱![]() 的中點,
的中點,
∴棱錐![]() 的體積是棱錐
的體積是棱錐![]() 體積的
體積的![]() ,
,
棱錐![]() 的體積是棱錐
的體積是棱錐![]() 的體積的
的體積的![]() ,
,
∴棱錐![]() 的體積與棱錐
的體積與棱錐![]() 的體積和為四棱錐
的體積和為四棱錐![]() 的體積的
的體積的![]() ;
;
棱錐![]() 的體積是棱錐
的體積是棱錐![]() 體積的
體積的![]() ,
,
棱錐![]() 的體積是棱錐
的體積是棱錐![]() 體積的
體積的![]() ,
,
∴棱錐![]() 的體積與棱錐
的體積與棱錐![]() 的體積和為四棱錐
的體積和為四棱錐![]() 的體積的
的體積的![]() ,
,
則中間剩下的棱錐![]() 的體積
的體積![]() 四棱錐
四棱錐![]() 的體積
的體積![]() 個四棱錐
個四棱錐![]() 的體積
的體積![]() 個四棱錐
個四棱錐![]() 的體積,
的體積,
則兩個棱錐![]() ,
,![]() 的體積之比是1:4.
的體積之比是1:4.
故答案為:![]() .
.


科目:高中數學 來源: 題型:
【題目】手機運動計步已經成為一種新時尚.某單位統計了職工一天行走步數(單位:百步),繪制出如下頻率分布直方圖:
(1)求直方圖中a的值,并由頻率分布直方圖估計該單位職工一天步行數的中位數;
(2)若該單位有職工200人,試估計職工一天行走步數不大于13000的人數;
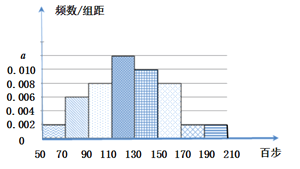
(3)在(2)的條件下,該單位從行走步數大于15000的3組職工中用分層抽樣的方法選取6人參加遠足拉練活動,再從6人中選取2人擔任領隊,求這兩人均來自區間(150,170]的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() (
(![]() )的左、右焦點為
)的左、右焦點為![]() ,右頂點為
,右頂點為![]() ,上頂點為
,上頂點為![]() .已知
.已知![]() .
.
(1)求橢圓的離心率;
(2)設![]() 為橢圓上異于其頂點的一點,以線段
為橢圓上異于其頂點的一點,以線段![]() 為直徑的圓經過點
為直徑的圓經過點![]() ,經過原點
,經過原點![]() 的直線
的直線![]() 與該圓相切,求直線
與該圓相切,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,直線
,直線![]() 不經過橢圓上頂點
不經過橢圓上頂點![]() ,與橢圓
,與橢圓![]() 交于
交于![]() ,
,![]() 不同兩點.
不同兩點.
(1)當![]() ,
,![]() 時,求橢圓
時,求橢圓![]() 的離心率的取值范圍;
的離心率的取值范圍;
(2)若![]() ,直線
,直線![]() 與
與![]() 的斜率之和為
的斜率之和為![]() ,證明:直線
,證明:直線![]() 過定點.
過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓![]()
![]() 的離心率為
的離心率為![]() ,且過點
,且過點![]() .
.
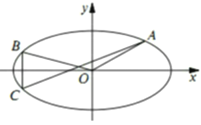
(I)求橢圓![]() 的標準方程;
的標準方程;
(II)設點![]() ,
,![]() 是橢圓
是橢圓![]() 上異于頂點的任意兩點,直線
上異于頂點的任意兩點,直線![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() 且
且![]() .
.
①求![]() 的值;
的值;
②設點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() ,試求直線
,試求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列![]() 的前n項和為
的前n項和為![]() ,對一切
,對一切![]() ,點
,點![]() 都在函數
都在函數![]() 的圖像上.
的圖像上.
(1)證明:當![]() 時,
時,![]() ;
;
(2)求數列![]() 的通項公式;
的通項公式;
(3)設![]() 為數列
為數列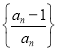 的前n項的積,若不等式
的前n項的積,若不等式![]() 對一切
對一切![]() 成立,求實數a的取值范圍.
成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在等腰Rt△ABC中,∠BAC=90°,腰長為2,D、E分別是邊AB、BC的中點,將△BDE沿DE翻折,得到四棱錐B﹣ADEC,且F為棱BC中點,BA![]() .
.
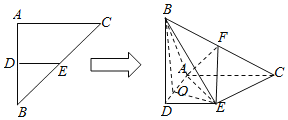
(1)求證:EF⊥平面BAC;
(2)在線段AD上是否存在一點Q,使得AF∥平面BEQ?若存在,求二面角Q﹣BE﹣A的余弦值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
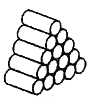
【題目】“垛積術”(隙積術)是由北宋科學家沈括在《夢溪筆談》中首創,南宋數學家楊輝、元代數學家朱世杰豐富和發展的一類數列求和方法,有菱草垛、方垛、芻童垛、三角垛等等,某倉庫中部分貨物堆放成如圖所示的“菱草垛”:自上而下,第一層1件,以后每一層比上一層多1件,最后一層是n件,已知第一層貨物單價1萬元,從第二層起,貨物的單價是上一層單價的![]() .若這堆貨物總價是
.若這堆貨物總價是![]() 萬元,則n的值為( )
萬元,則n的值為( )
A. 7B. 8C. 9D. 10
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com