
【題目】某地隨著經濟的發展,居民收入逐年增長,下表是該地一建設銀行連續五年的儲蓄存款(年底余額),如下表1:
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
儲蓄存款y(千億元) | 5 | 6 | 7 | 8 | 10 |
為了研究計算的方便,工作人員將上表的數據進行了處理, ![]() 得到下表2:
得到下表2:
時間代號t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
(Ⅰ)求z關于t的線性回歸方程;
(Ⅱ)用所求回歸方程預測到2020年年底,該地儲蓄存款額可達多少?
(附:對于線性回歸方程![]() ,其中
,其中 )
)
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=﹣x3+ax2+bx+c圖象上的點P(1,m)處的切線方程為y=﹣3x+1
(1)若函數f(x)在x=﹣2時有極值,求f(x)的表達式.
(2)若函數f(x)在區間[﹣2,0]上單調遞增,求實數b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]()
![]() 的
的
部分圖像如圖所示.
(Ⅰ)求函數![]() 的解析式及
的解析式及![]() 圖像的對稱軸方程;
圖像的對稱軸方程;
(Ⅱ)把函數![]() 圖像上點的橫坐標擴大到原來的
圖像上點的橫坐標擴大到原來的![]() 倍(縱坐標不變),再向左平移
倍(縱坐標不變),再向左平移
![]() 個單位,得到函數
個單位,得到函數![]() 的圖象,求關于
的圖象,求關于![]() 的方程
的方程![]()
在![]() 時所有的實數根之和.
時所有的實數根之和.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數f(x)=sin2x的圖象向右平移φ(0<φ< ![]() )個單位后得到函數g(x)的圖象.若對滿足|f(x1)﹣g(x2)|=2的x1、x2 , 有|x1﹣x2|min=
)個單位后得到函數g(x)的圖象.若對滿足|f(x1)﹣g(x2)|=2的x1、x2 , 有|x1﹣x2|min= ![]() ,則φ=( )
,則φ=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,已知橢圓![]() 的半焦距為c,且過點
的半焦距為c,且過點![]() ,原點O到經過兩點(c,0),(0,b)的直線的距離為
,原點O到經過兩點(c,0),(0,b)的直線的距離為![]() .
.
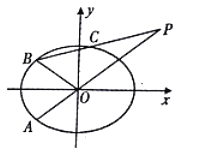
(1)求橢圓E的方程;
(2)A為橢圓E上異于頂點的一點,點P滿足![]() ,過點P的直線交橢圓E于B,C兩點,且
,過點P的直線交橢圓E于B,C兩點,且![]() ,若直線OA,OB的斜率之積為
,若直線OA,OB的斜率之積為![]() ,求證:
,求證: ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com