
【題目】已知數列![]() 的各項均為正數,
的各項均為正數,![]() ,且對任意
,且對任意![]() ,都有
,都有![]() ,數列
,數列![]() 前n項的和
前n項的和![]() .
.
(1)若數列![]() 是等比數列,求
是等比數列,求![]() 的值和
的值和![]() ;
;
(2)若數列![]() 是等差數列,求
是等差數列,求![]() 和
和![]() 的關系式;
的關系式;
(3)![]() ,當
,當![]() 時,求證:
時,求證: ![]() 是一個常數.
是一個常數.
 寒假大串聯黃山書社系列答案
寒假大串聯黃山書社系列答案科目:高中數學 來源: 題型:
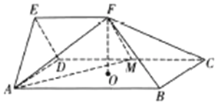
【題目】如圖,楔形幾何體![]() 由一個三棱柱截去部分后所得,底面
由一個三棱柱截去部分后所得,底面![]() 側面
側面![]() ,
,![]() ,楔面
,楔面![]() 是邊長為2的正三角形,點
是邊長為2的正三角形,點![]() 在側面
在側面![]() 的射影是矩形
的射影是矩形![]() 的中心
的中心![]() ,點
,點![]() 在
在![]() 上,且
上,且![]()
(1)證明:![]() 平面
平面![]() ;
;
(2)求楔面![]() 與側面
與側面![]() 所成二面角的余弦值.
所成二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中錯誤的是( )
A.命題“若![]() ,則
,則![]() ”的逆否命題是真命題
”的逆否命題是真命題
B.命題“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
C.若![]() 為真命題,則
為真命題,則![]() 為真命題
為真命題
D.在![]() 中,“
中,“![]() ”是“
”是“![]() ”的充要條件
”的充要條件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的前n項和為
的前n項和為![]() ,且滿足
,且滿足![]() ,數列
,數列![]() 中,
中,![]() ,對任意正整數
,對任意正整數![]() ,
, .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)是否存在實數![]() ,使得數列
,使得數列![]() 是等比數列?若存在,請求出實數
是等比數列?若存在,請求出實數![]() 及公比q的值,若不存在,請說明理由;
及公比q的值,若不存在,請說明理由;
(3)求數列![]() 前n項和
前n項和![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一次購物抽獎活動中,已知某10張獎券中有6張有獎,其余4張沒有獎,且有獎的6張獎券每張均可獲得價值10元的獎品.某顧客從此10張獎券中任意抽取3張.
(1)求該顧客中獎的概率;
(2)若約定抽取的3張獎券都有獎時,還要另獎價值6元的獎品,求該顧客獲得的獎品總價值![]() (元)的分布列和均值.
(元)的分布列和均值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,直線
,直線![]() 不經過橢圓上頂點
不經過橢圓上頂點![]() ,與橢圓
,與橢圓![]() 交于
交于![]() ,
,![]() 不同兩點.
不同兩點.
(1)當![]() ,
,![]() 時,求橢圓
時,求橢圓![]() 的離心率的取值范圍;
的離心率的取值范圍;
(2)若![]() ,直線
,直線![]() 與
與![]() 的斜率之和為
的斜率之和為![]() ,證明:直線
,證明:直線![]() 過定點.
過定點.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com