
 已知正四面體ABCD中,E是AB的中點,則異面直線CE與BD所成角的余弦值為( )
已知正四面體ABCD中,E是AB的中點,則異面直線CE與BD所成角的余弦值為( )| A. | $\frac{\sqrt{3}}{6}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 0 |
分析 利用中點,取AD的中點為F,連接EF,CE則EF∥BD,所以異面直線CE與EF所成的夾角就是CE與BD所成的夾角,利用余弦定理求解.
解答 解:設AD的中點為F,連接EF,CE,則EF∥BD,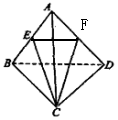
∴異面直線CE與EF所成的夾角就是CE與BD所成的夾角,
由題意:設正四面體ABCD的棱長為2a,則EF=a,CE=CF=$\sqrt{3}$a,
由余弦定理可得cos∠CEF=$\frac{E{F}^{2}+E{C}^{2}-C{F}^{2}}{2×EF×EC}=\frac{\sqrt{3}}{6}$
故選A
點評 本題考查兩條異面直線所成角的大小的求法,是中檔題,解題時要認真審題,注意空間思維能力的培養.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:選擇題

| A. | $\frac{7}{8}$ | B. | $\frac{15}{16}$ | C. | $\frac{31}{32}$ | D. | $\frac{63}{64}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | y=$±\frac{5}{4}$x | B. | y=$±\frac{4}{5}$x | C. | y=$±\frac{16}{25}$x | D. | y=±$\frac{25}{16}$x |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
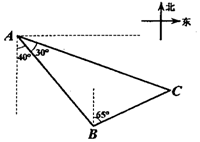 如圖所示,一艘海輪從A處出發,以每小時40海里的速度沿南偏東40°方向直線航行,30分鐘后到達B處,在C處有一座燈塔,海輪在A處觀察燈塔,其方向是南偏東70°,在B處觀察燈塔,其方向是北偏東65°,那么B、C兩點間的距離是10$\sqrt{2}$海里.
如圖所示,一艘海輪從A處出發,以每小時40海里的速度沿南偏東40°方向直線航行,30分鐘后到達B處,在C處有一座燈塔,海輪在A處觀察燈塔,其方向是南偏東70°,在B處觀察燈塔,其方向是北偏東65°,那么B、C兩點間的距離是10$\sqrt{2}$海里.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com