
【題目】2012年12月18日,作為全國首批開展空氣質量新標準監測的74個城市之一,鄭州市正式發布![]() 數據.資料表明,近幾年來,鄭州市霧霾治理取得了很大成效,空氣質量與前幾年相比得到了很大改善.鄭州市設有9個監測站點監測空氣質量指數(
數據.資料表明,近幾年來,鄭州市霧霾治理取得了很大成效,空氣質量與前幾年相比得到了很大改善.鄭州市設有9個監測站點監測空氣質量指數(![]() ),其中在輕度污染區、中度污染區、重度污染區分別設有2,5,2個監測站點,以9個站點測得的
),其中在輕度污染區、中度污染區、重度污染區分別設有2,5,2個監測站點,以9個站點測得的![]() 的平均值為依據,播報我市的空氣質量.
的平均值為依據,播報我市的空氣質量.
(1)若某日播報的![]() 為118,已知輕度污染區
為118,已知輕度污染區![]() 的平均值為74,中度污染區
的平均值為74,中度污染區![]() 的平均值為114,求重度污染區
的平均值為114,求重度污染區![]() 的平均值;
的平均值;
(2)如圖是2018年11月的30天中![]() 的分布,11月份僅有一天
的分布,11月份僅有一天![]() 在
在![]() 內.
內.
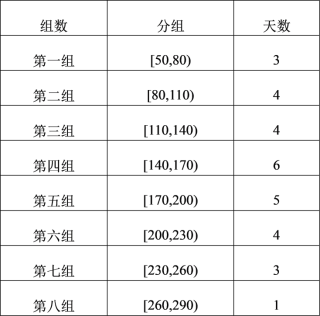
①鄭州市某中學利用每周日的時間進行社會實踐活動,以公布的![]() 為標準,如果
為標準,如果![]() 小于180,則去進行社會實踐活動.以統計數據中的頻率為概率,求該校周日進行社會實踐活動的概率;
小于180,則去進行社會實踐活動.以統計數據中的頻率為概率,求該校周日進行社會實踐活動的概率;
②在“創建文明城市”活動中,驗收小組把鄭州市的空氣質量作為一個評價指標,從當月的空氣質量監測數據中抽取3天的數據進行評價,設抽取到![]() 不小于180的天數為
不小于180的天數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
 一諾書業暑假作業快樂假期云南美術出版社系列答案
一諾書業暑假作業快樂假期云南美術出版社系列答案科目:高中數學 來源: 題型:
【題目】2020年春節,一場突如其來的新型冠狀病毒感染的肺炎疫情,牽動著我們每個人的心,嚴重擾亂了大家的正常生活,在全國人民的共同努力下,疫情得到了有效的控制.已知某市A,B,C三個小區的志愿者人數分別為60,40,20,現采用分層抽樣的方法從這120名志愿者中隨機抽取6人去支援夕陽紅敬老院.若再從這6人中隨機抽取2名作為負責人,則這2名志愿者來自不同小區的概率是________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)求f(x)的最大值;
(2)設函數![]() ,若對任意實數
,若對任意實數![]() ,當
,當![]() 時,函數
時,函數![]() 的最大值為
的最大值為![]() ,求a的取值范圍;
,求a的取值范圍;
(3)若數列![]() 的各項均為正數,
的各項均為正數,![]() ,
,![]() .求證:
.求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大型商場的空調在1月到5月的銷售量與月份相關,得到的統計數據如下表:
月份 | 1 | 2 | 3 | 4 | 5 |
銷量 | 0.6 | 0.8 | 1.2 | 1.6 | 1.8 |
(1)經分析發現1月到5月的銷售量可用線性回歸模型擬合該商場空調的月銷量![]() (百件)與月份
(百件)與月份![]() 之間的相關關系.請用最小二乘法求
之間的相關關系.請用最小二乘法求![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ,并預測6月份該商場空調的銷售量;
,并預測6月份該商場空調的銷售量;
(2)若該商場的營銷部對空調進行新一輪促銷,對7月到12月有購買空調意愿的顧客進行問卷調查.假設該地擬購買空調的消費群體十分龐大,經過營銷部調研機構對其中的500名顧客進行了一個抽樣調查,得到如下一份頻數表:
有購買意愿對應的月份 | 7 | 8 | 9 | 10 | 11 | 12 |
頻數 | 60 | 80 | 120 | 130 | 80 | 30 |
現采用分層抽樣的方法從購買意愿的月份在7月與12月的這90名顧客中隨機抽取6名,再從這6人中隨機抽取3人進行跟蹤調查,求抽出的3人中恰好有2人是購買意愿的月份是12月的概率.
參考公式與數據:線性回歸方程![]() ,其中
,其中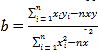 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某度假酒店為了解會員對酒店的滿意度,從中抽取50名會員進行調查,把會員對酒店的“住宿滿意度”與“餐飲滿意度”都分為五個評分標準:1分(很不滿意);2分(不滿意);3分(一般);4分(滿意);5分(很滿意).其統計結果如下表(住宿滿意度為![]() ,餐飲滿意度為
,餐飲滿意度為![]() )
)

(1)求“住宿滿意度”分數的平均數;
(2)求“住宿滿意度”為3分時的5個“餐飲滿意度”人數的方差;
(3)為提高對酒店的滿意度,現從![]() 且
且![]() 的會員中隨機抽取2人征求意見,求至少有1人的“住宿滿意度”為2的概率.
的會員中隨機抽取2人征求意見,求至少有1人的“住宿滿意度”為2的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】健身館某項目收費標準為每次60元,現推出會員優惠活動:具體收費標準如下:
消費次數 | 第1次 | 第2次 | 第3次 | 不少于4次 |
收費比例 | 0.95 | 0.90 | 0.85 | 0.80 |
現隨機抽取了100位會員統計它們的消費次數,得到數據如下:
消費次數 | 1次 | 2次 | 3次 | 不少于4次 |
頻數 | 60 | 25 | 10 | 5 |
假設該項目的成本為每次30元,根據給出的數據回答下列問題:
(1)估計1位會員至少消費兩次的概率
(2)某會員消費4次,求這4次消費獲得的平均利潤;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com