
【題目】已知函數![]() .
.
(1)若![]() ,則當
,則當![]() 時,討論
時,討論![]() 的單調性;
的單調性;
(2)若![]() ,且當
,且當![]() 時,不等式
時,不等式![]() 在區間
在區間![]() 上有解,求實數
上有解,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)答案見解析;(2)![]() .
.
【解析】試題分析:
(1)函數![]() 的定義域為
的定義域為![]() ,且
,且![]() ,
,![]() .分類討論可得:
.分類討論可得:
當![]() 時,
時,![]() 在
在![]() 內單調遞減;
內單調遞減;
當![]() 時,
時,![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增;
上單調遞增;
當![]() 時,
時,![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
(2)原問題等價于當![]() 時,
時,![]() 在區間
在區間![]() 上的最大值
上的最大值![]() .
.
且![]() ,則
,則![]() .分類討論
.分類討論![]() 和
和![]() 兩種情況可得
兩種情況可得![]() .據此求解關于實數a的不等式可得實數
.據此求解關于實數a的不等式可得實數![]() 的取值范圍是
的取值范圍是![]() .
.
試題解析:
(1)函數![]() 的定義域為
的定義域為![]() ,由
,由![]() 得
得![]() ,
,
所以![]() .
.
當![]() 時,
時,![]() ,
,![]() 在
在![]() 內單調遞減;
內單調遞減;
當![]() 時,
時,![]() 或
或![]() ,
,
所以,![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增;
上單調遞增;
當![]() 時,
時,![]() 或
或![]() ,
,
所以,![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
(2)由題意,當![]() 時,
時,![]() 在區間
在區間![]() 上的最大值
上的最大值![]() .
.
當![]() 時,
時,![]() ,
,
則![]() .
.
①當![]() 時,
時,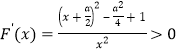 ,
,
故![]() 在
在![]() 上單調遞增,
上單調遞增,![]() ;
;
②當![]() 時,設
時,設![]() 的兩根分別為
的兩根分別為![]() ,
,
則![]() ,所以在
,所以在![]() 上
上![]() ,
,
故![]() 在
在![]() 上單調遞增,
上單調遞增,![]() .
.
綜上,當![]() 時,
時,![]() 在區間
在區間![]() 上的最大值
上的最大值![]() ,
,
解得![]() ,所以實數
,所以實數![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() :
:![]() (
(![]() )的離心率
)的離心率![]() ,左、右焦點分別為
,左、右焦點分別為![]() ,
,![]() ,過
,過![]() ,
,![]() 分別作兩條相互垂直的直線
分別作兩條相互垂直的直線![]() ,
,![]() ,分別交橢圓
,分別交橢圓![]() 于
于![]() ,
,![]() ,
,![]() ,
,![]() 四點,
四點,![]() ,
,![]() 的交點為
的交點為![]() ,三角形
,三角形![]() 面積的最大值為1.
面積的最大值為1.
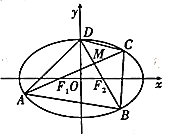
(1)求橢圓![]() 的方程;
的方程;
(2)當四邊形![]() 的面積
的面積![]() 最小時,求點
最小時,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,下面結論正確的是( )
,下面結論正確的是( )
A.若![]() ,
,![]() ,且
,且![]() 的最小值為π,則ω=2
的最小值為π,則ω=2
B.存在ω∈(1,3),使得f(x)的圖象向右平移![]() 個單位長度后得到的圖象關于y軸對稱
個單位長度后得到的圖象關于y軸對稱
C.若f(x)在![]() 上恰有7個零點,則ω的取值范圍是
上恰有7個零點,則ω的取值范圍是![]()
D.若f(x)在![]() 上單調遞增,則ω的取值范圍是(0,
上單調遞增,則ω的取值范圍是(0,![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2012年12月18日,作為全國首批開展空氣質量新標準監測的74個城市之一,鄭州市正式發布![]() 數據.資料表明,近幾年來,鄭州市霧霾治理取得了很大成效,空氣質量與前幾年相比得到了很大改善.鄭州市設有9個監測站點監測空氣質量指數(
數據.資料表明,近幾年來,鄭州市霧霾治理取得了很大成效,空氣質量與前幾年相比得到了很大改善.鄭州市設有9個監測站點監測空氣質量指數(![]() ),其中在輕度污染區、中度污染區、重度污染區分別設有2,5,2個監測站點,以9個站點測得的
),其中在輕度污染區、中度污染區、重度污染區分別設有2,5,2個監測站點,以9個站點測得的![]() 的平均值為依據,播報我市的空氣質量.
的平均值為依據,播報我市的空氣質量.
(1)若某日播報的![]() 為118,已知輕度污染區
為118,已知輕度污染區![]() 的平均值為74,中度污染區
的平均值為74,中度污染區![]() 的平均值為114,求重度污染區
的平均值為114,求重度污染區![]() 的平均值;
的平均值;
(2)如圖是2018年11月的30天中![]() 的分布,11月份僅有一天
的分布,11月份僅有一天![]() 在
在![]() 內.
內.
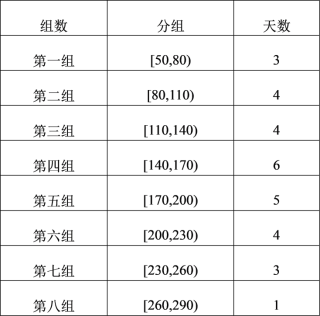
①鄭州市某中學利用每周日的時間進行社會實踐活動,以公布的![]() 為標準,如果
為標準,如果![]() 小于180,則去進行社會實踐活動.以統計數據中的頻率為概率,求該校周日進行社會實踐活動的概率;
小于180,則去進行社會實踐活動.以統計數據中的頻率為概率,求該校周日進行社會實踐活動的概率;
②在“創建文明城市”活動中,驗收小組把鄭州市的空氣質量作為一個評價指標,從當月的空氣質量監測數據中抽取3天的數據進行評價,設抽取到![]() 不小于180的天數為
不小于180的天數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的焦點為F,過點F,斜率為1的直線與拋物線C交于點A,B,且
的焦點為F,過點F,斜率為1的直線與拋物線C交于點A,B,且![]() .
.
(1)求拋物線C的方程;
(2)過點Q(1,1)作直線交拋物線C于不同于R(1,2)的兩點D、E,若直線DR,ER分別交直線![]() 于M,N兩點,求|MN|取最小值時直線DE的方程.
于M,N兩點,求|MN|取最小值時直線DE的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,且過點
,且過點 .
.
(1)求![]() 的方程;
的方程;
(2)是否存在直線![]() 與
與![]() 相交于
相交于![]() 兩點,且滿足:①
兩點,且滿足:①![]() 與
與![]() (
(![]() 為坐標原點)的斜率之和為2;②直線
為坐標原點)的斜率之和為2;②直線![]() 與圓
與圓![]() 相切,若存在,求出
相切,若存在,求出![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】千百年來,我國勞動人民在生產實踐中根據云的形狀、走向、速度、厚度、顏色等的變化,總結了豐富的“看云識天氣”的經驗,并將這些經驗編成諺語,如“天上鉤鉤云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同學為了驗證“日落云里走,雨在半夜后”,觀察了所在地區A的100天日落和夜晚天氣,得到如下![]() 列聯表:
列聯表:
夜晚天氣 日落云里走 | 下雨 | 未下雨 |
出現 | 25 | 5 |
未出現 | 25 | 45 |
臨界值表 | ||||
P( | 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
并計算得到![]() ,下列小波對地區A天氣判斷不正確的是( )
,下列小波對地區A天氣判斷不正確的是( )
A.夜晚下雨的概率約為![]()
B.未出現“日落云里走”夜晚下雨的概率約為![]()
C.有![]() 的把握認為“‘日落云里走’是否出現”與“當晚是否下雨”有關
的把握認為“‘日落云里走’是否出現”與“當晚是否下雨”有關
D.出現“日落云里走”,有![]() 的把握認為夜晚會下雨
的把握認為夜晚會下雨
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com