
【題目】已知拋物線![]() 的焦點為F,過點F,斜率為1的直線與拋物線C交于點A,B,且
的焦點為F,過點F,斜率為1的直線與拋物線C交于點A,B,且![]() .
.
(1)求拋物線C的方程;
(2)過點Q(1,1)作直線交拋物線C于不同于R(1,2)的兩點D、E,若直線DR,ER分別交直線![]() 于M,N兩點,求|MN|取最小值時直線DE的方程.
于M,N兩點,求|MN|取最小值時直線DE的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)過點F且斜率為![]() 的直線方程與拋物線的方程聯立,利用
的直線方程與拋物線的方程聯立,利用![]() 求得
求得![]() 的值,即可求得拋物線
的值,即可求得拋物線![]() 的方程;
的方程;
(2)設D(x1,y1),E(x2,y2),直線DE的方程為![]() ,直線
,直線![]() 的方程為
的方程為![]() ,由題意求出
,由題意求出![]() 得值,建立
得值,建立![]() 的解析式,再求出
的解析式,再求出![]() 的最小值以及直線
的最小值以及直線![]() 的方程.
的方程.
(1)拋物線![]() 的焦點為
的焦點為![]() ,
,
直線方程為:![]() ,
,
代入![]() 中,消去y得:
中,消去y得: ![]() ,
,
設A(x1,y1),B(x2,y2),則有![]() ,
,
由![]() ,得
,得![]() ,即
,即![]() ,解得
,解得![]() ,
,
所以拋物線C的方程為:![]() ;
;
(2)設D(x1,y1),E(x2,y2),直線DE的方程為![]() ,如圖所示,
,如圖所示,
由![]() ,消去
,消去![]() ,整理得:
,整理得:![]() ,
,
∴![]() ,
,
設直線DR的方程為![]() ,
,
由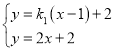 ,解得點M的橫坐標
,解得點M的橫坐標![]() ,
,
又k1=![]() =
=![]() ,∴xM=
,∴xM=![]() =-
=-![]() ,
,
同理點N的橫坐標![]() ,
,
![]() =4
=4![]() ,
,
∴|MN|=![]() |xM-xN|=
|xM-xN|=![]() |-
|-![]() +
+![]() |=2
|=2![]() |
|![]() |=
|=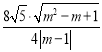 =
=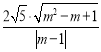 ,
,
令![]() ,則
,則![]() ,
,
∴|MN|=![]()
![]() =
=![]()
![]() =
=![]()
![]() ≥
≥![]()
![]() =
=![]() ,
,
所以當![]() ,即
,即![]() 時,|MN|取最小值為
時,|MN|取最小值為![]() ,
,
此時直線DE的方程為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】2019年泉州市農村電商發展迅猛,成為創新農產品交易方式、增加農民收入、引導農業供給側結構性改革、促進鄉村振興的重要力量,成為鄉村振興的新引擎.2019年大學畢業的李想,選擇回到家鄉泉州自主創業,他在網上開了一家水果網店.2019年雙十一期間,為了增加水果銷量,李想設計了下面兩種促銷方案:方案一:購買金額每滿120元,即可抽獎一次,中獎可獲得20元,每次中獎的概率為![]() (
(![]() ),假設每次抽獎相互獨立.方案二:購買金額不低于180元時,即可優惠
),假設每次抽獎相互獨立.方案二:購買金額不低于180元時,即可優惠![]() 元,并在優惠后的基礎上打九折.
元,并在優惠后的基礎上打九折.
(1)在促銷方案一中,設每10個抽獎人次中恰有6人次中獎的概率為![]() ,求
,求![]() 的最大值點
的最大值點![]() ;
;
(2)若促銷方案二中,李想每筆訂單得到的金額均不低于促銷前總價的八折,求![]() 的最大值;
的最大值;
(3)以(1)中確定的![]() 作為
作為![]() 的值,且當
的值,且當![]() 取最大值時,若某位顧客一次性購買了360元,則該顧客應選擇哪種促銷方案?請說明理由.
取最大值時,若某位顧客一次性購買了360元,則該顧客應選擇哪種促銷方案?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設點![]() 為平面直角坐標系
為平面直角坐標系![]() 中的一個動點(其中
中的一個動點(其中![]() 為坐標系原點),點
為坐標系原點),點![]() 到定點
到定點![]() 的距離比到直線
的距離比到直線![]() 的距離大1,動點
的距離大1,動點![]() 的軌跡方程為
的軌跡方程為![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)若過點![]() 的直線
的直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 、
、![]() 兩點.
兩點.
①若![]() ,求直線
,求直線![]() 的直線方程;
的直線方程;
②分別過點![]() ,
,![]() 作曲線
作曲線![]() 的切線且交于點
的切線且交于點![]() ,是否存在以
,是否存在以![]() 為圓心,以
為圓心,以![]() 為半徑的圓與經過點
為半徑的圓與經過點![]() 且垂直于直線
且垂直于直線![]() 的直線
的直線![]() 相交于
相交于![]() 、
、![]() 兩點,求
兩點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大型商場的空調在1月到5月的銷售量與月份相關,得到的統計數據如下表:
月份 | 1 | 2 | 3 | 4 | 5 |
銷量 | 0.6 | 0.8 | 1.2 | 1.6 | 1.8 |
(1)經分析發現1月到5月的銷售量可用線性回歸模型擬合該商場空調的月銷量![]() (百件)與月份
(百件)與月份![]() 之間的相關關系.請用最小二乘法求
之間的相關關系.請用最小二乘法求![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ,并預測6月份該商場空調的銷售量;
,并預測6月份該商場空調的銷售量;
(2)若該商場的營銷部對空調進行新一輪促銷,對7月到12月有購買空調意愿的顧客進行問卷調查.假設該地擬購買空調的消費群體十分龐大,經過營銷部調研機構對其中的500名顧客進行了一個抽樣調查,得到如下一份頻數表:
有購買意愿對應的月份 | 7 | 8 | 9 | 10 | 11 | 12 |
頻數 | 60 | 80 | 120 | 130 | 80 | 30 |
現采用分層抽樣的方法從購買意愿的月份在7月與12月的這90名顧客中隨機抽取6名,再從這6人中隨機抽取3人進行跟蹤調查,求抽出的3人中恰好有2人是購買意愿的月份是12月的概率.
參考公式與數據:線性回歸方程![]() ,其中
,其中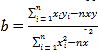 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() +
+![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為![]() ,直線l:x+2y=4與橢圓有且只有一個交點T.
,直線l:x+2y=4與橢圓有且只有一個交點T.
(I)求橢圓C的方程和點T的坐標;
(Ⅱ)O為坐標原點,與OT平行的直線l′與橢圓C交于不同的兩點A,B,直線l′與直線l交于點P,試判斷![]() 是否為定值,若是請求出定值,若不是請說明理由.
是否為定值,若是請求出定值,若不是請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區經過一年的新農村建設,農村的經濟收入增加了一倍.實現翻番.為更好地了解該地區農村的經濟收入變化情況,統計了該地區新農村建設前后農村的經濟收入構成比例.得到如下餅圖:

則下面結論中不正確的是
A. 新農村建設后,種植收入減少
B. 新農村建設后,其他收入增加了一倍以上
C. 新農村建設后,養殖收入增加了一倍
D. 新農村建設后,養殖收入與第三產業收入的總和超過了經濟收入的一半
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】袋中裝有黑球和白球共7個,從中任取2個球都是白球的概率為![]() ,現有甲,乙二人從袋中輪流摸取1球,甲先取,乙后取,然后甲再取,……,取后不放回,直到兩人中有一人取到白球即終止,每個球在每一次被取出的機會是等可能的.
,現有甲,乙二人從袋中輪流摸取1球,甲先取,乙后取,然后甲再取,……,取后不放回,直到兩人中有一人取到白球即終止,每個球在每一次被取出的機會是等可能的.
(Ⅰ)求袋中原有白球的個數:
(Ⅱ)求取球次數![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com