
【題目】設![]() 為數列
為數列![]() 的前
的前![]() 項和,對任意的
項和,對任意的![]() ,都有
,都有![]() (
(![]() 為正常數).
為正常數).
(1)求證:數列![]() 是等比數列;
是等比數列;
(2)數列![]() 滿足
滿足![]() ,
,![]() ,求數列
,求數列![]() 的通項公式;
的通項公式;
(3)在滿足(2)的條件下,求數列![]() 的前
的前![]() 項和
項和![]() .
.
【答案】(1)詳見解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
試題分析:(1)利用![]() 與
與![]() 之間的關系
之間的關系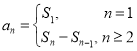 ,對
,對![]() 分兩種情況討論,
分兩種情況討論,![]() 時,求
時,求![]() 的值,
的值,![]() 時,利用
時,利用![]() 得出
得出![]() 與
與![]() 之間的關系,進而利用定義證明數列
之間的關系,進而利用定義證明數列![]() 為等比數列;
為等比數列;
(2)在(1)的條件下求出![]() 的值,然后根據數列
的值,然后根據數列![]() 的遞推公式的結構利用倒數法得到數列
的遞推公式的結構利用倒數法得到數列![]() 為等差數列,通過求處等差數列
為等差數列,通過求處等差數列![]() 的通項公式求出數列
的通項公式求出數列![]() 的通項公式;(3)利用(2)中數列
的通項公式;(3)利用(2)中數列![]() 的通項公式,并根據數列
的通項公式,并根據數列![]() 的通項公式的結構選擇錯位相減法求數列
的通項公式的結構選擇錯位相減法求數列![]() 的前
的前![]() 項和
項和![]() .
.
試題解析:(1)證明:當![]() 時,
時,![]() ,解得
,解得![]() . 1分
. 1分
當![]() 時,
時,![]() .即
.即![]() . 2分
. 2分
又![]() 為常數,且
為常數,且![]() ,∴
,∴![]() . 3分
. 3分
∴數列![]() 是首項為1,公比為
是首項為1,公比為![]() 的等比數列. 4分
的等比數列. 4分
(2)![]() 5分 ∵
5分 ∵![]() ,∴
,∴![]()
![]() ,即
,即![]() . 7分
. 7分
∴![]() 是首項為
是首項為![]() ,公差為1的等差數列. 8分
,公差為1的等差數列. 8分
∴![]() ,即
,即![]() . 9分
. 9分
(3)由(2)知![]() ,則
,則![]() .
.
所以![]() , 10分
, 10分
即![]() , ① 11分
, ① 11分
則![]() , ② 12分
, ② 12分
②-①得![]() , 13分
, 13分
故![]() . 14分
. 14分


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:
【題目】(1)求過直線l1:x-2y+3=0與直線l2:2x+3y-8=0的交點,且到點P(0,4)的距離為2的直線方程.
(2)設直線l的方程為(a+1)x+y+2-a=0(a∈R).若l在兩坐標軸上的截距相等,求l的方程;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人玩數字游戲,先由甲任想一個數字記為![]() ,再由乙猜甲剛才想的數字把乙想的數字記為
,再由乙猜甲剛才想的數字把乙想的數字記為![]() ,且
,且![]() ,
, ![]() ,記
,記![]() .
.
(1)求![]() 的概率;
的概率;
(2)若![]() ,則稱“甲乙心有靈犀”,求“甲乙心有靈犀”的概率.
,則稱“甲乙心有靈犀”,求“甲乙心有靈犀”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知棱長為l的正方體![]() 中,E,F,M分別是AB、AD、
中,E,F,M分別是AB、AD、![]() 的中點,又P、Q分別在線段
的中點,又P、Q分別在線段![]() 上,且
上,且![]() ,設面
,設面![]() 面MPQ=
面MPQ=![]() ,則下列結論中不成立的是( )
,則下列結論中不成立的是( )

A.![]() 面ABCD
面ABCD
B.![]() AC
AC
C.面MEF與面MPQ不垂直
D.當x變化時,![]() 不是定直線
不是定直線
查看答案和解析>>
科目:高中數學 來源: 題型:
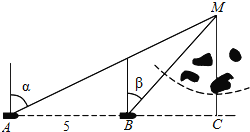
【題目】如圖,一船由西向東航行,在A處測得某島M的方位角為α,前進5km后到達B處,測得島M的方位角為β.已知該島周圍3km內有暗礁,現該船繼續東行.
(1)若α=2β=60°,問該船有無觸礁危險?
(2)當α與β滿足什么條件時,該船沒有觸礁的危險?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場預計全年分批購入每臺2000元的電視機共3600臺.每批都購入![]() 臺(
臺(![]() 是自然數)且每批均需付運費400元.貯存購入的電視機全年所需付的保管費 與每批購入電視機的總價值(不含運費)成正比.若每批購入400臺,則全年需用去運輸和保管總費用43600元.現在全年只有24000元資金可以支付這筆費用,請問,能否恰當安排每批進貨數量,使資金夠用?寫出你的結論,并說明理由.
是自然數)且每批均需付運費400元.貯存購入的電視機全年所需付的保管費 與每批購入電視機的總價值(不含運費)成正比.若每批購入400臺,則全年需用去運輸和保管總費用43600元.現在全年只有24000元資金可以支付這筆費用,請問,能否恰當安排每批進貨數量,使資金夠用?寫出你的結論,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com